Selection and the Roy Model in the Neolithic Transition

Authors
Affiliations

Nurfatima Jandarova

University of Minnesota, Department of Economics

Aldo Rustichini

European Social Science Genetics Network Conference II

Published

May 11, 2023

Introduction

Technological and climate shift

  • direct effect: incentives and decisions

  • indirect effect: population distribution

This paper

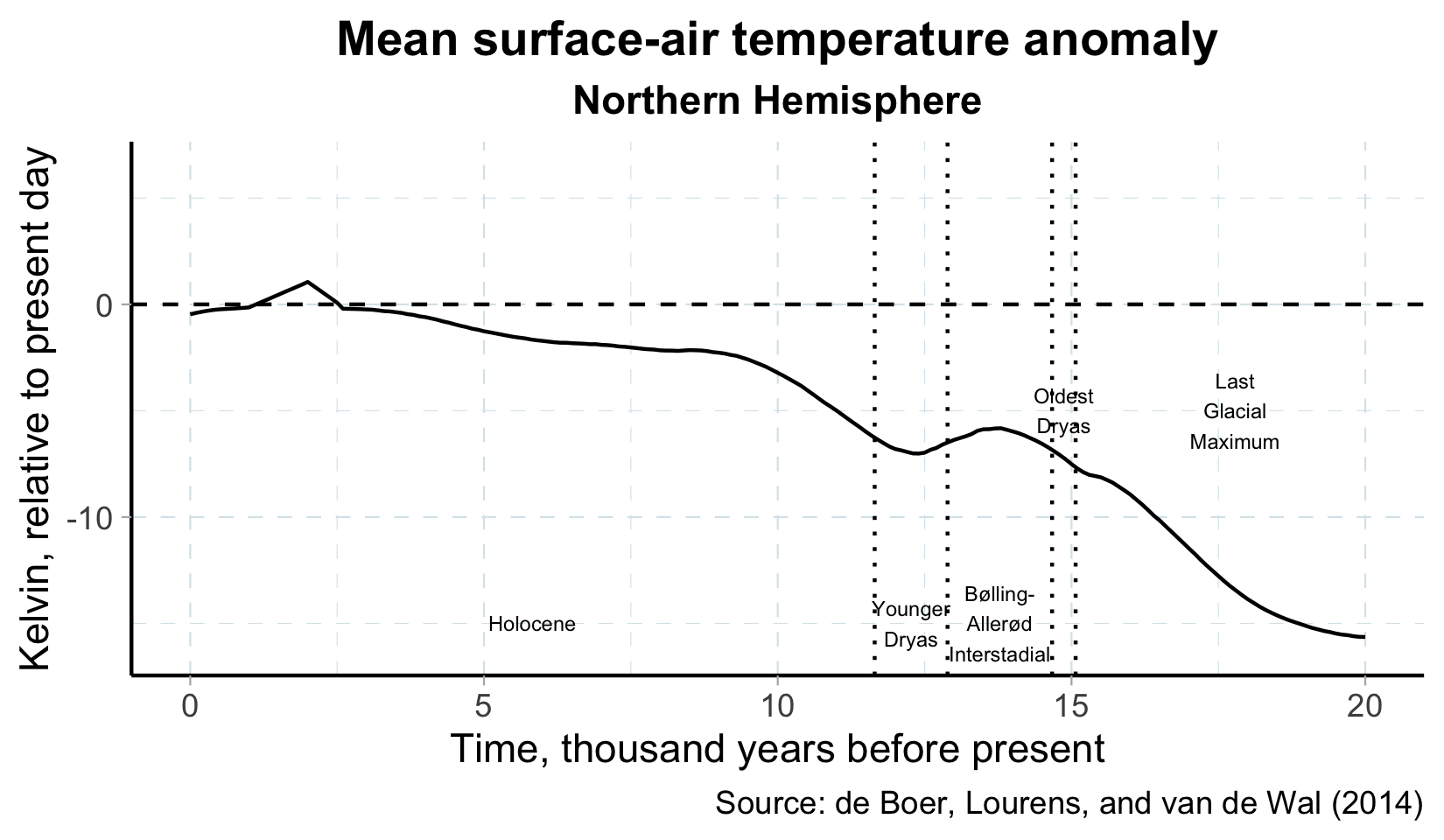
  • Climate shift and adoption of agriculture over the past 14,000 years

  • Link selection to economic activity choice (farming vs foraging)

  • Evolution in population distribution

  • Impact: current choices depend on actions of past generations

Contributions

Polygenic selection: Berg and Coop (2014); Racimo, Berg, and Pickrell (2018); Guo, Yang, and Visscher (2018); Cox et al. (2019); S. Mathieson and Mathieson (2018); Uricchio (2020); I. Mathieson (2021); Song et al. (2021); Stern et al. (2021); Yair and Coop (2022)

Emphasise the role of genotype distribution

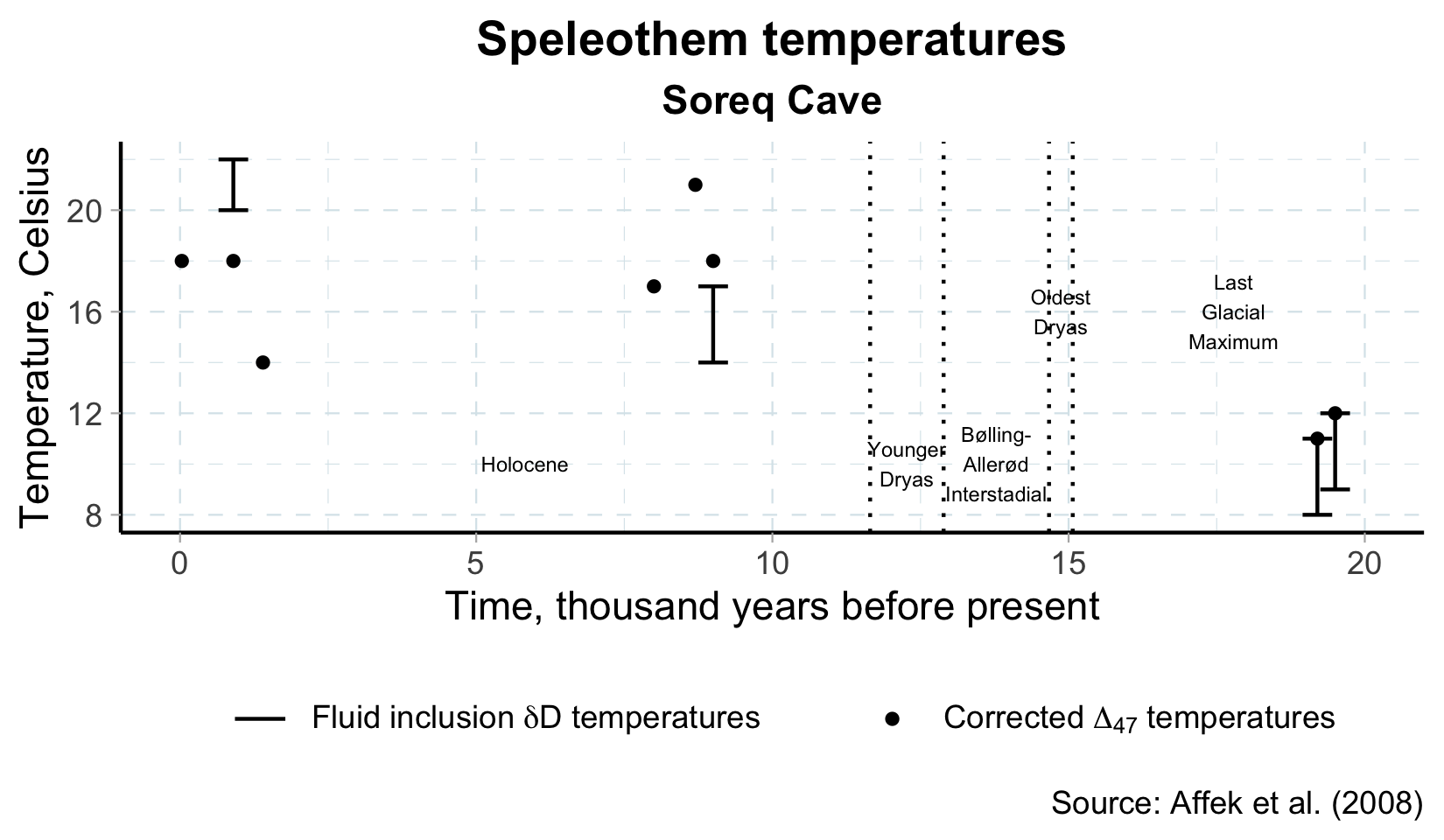
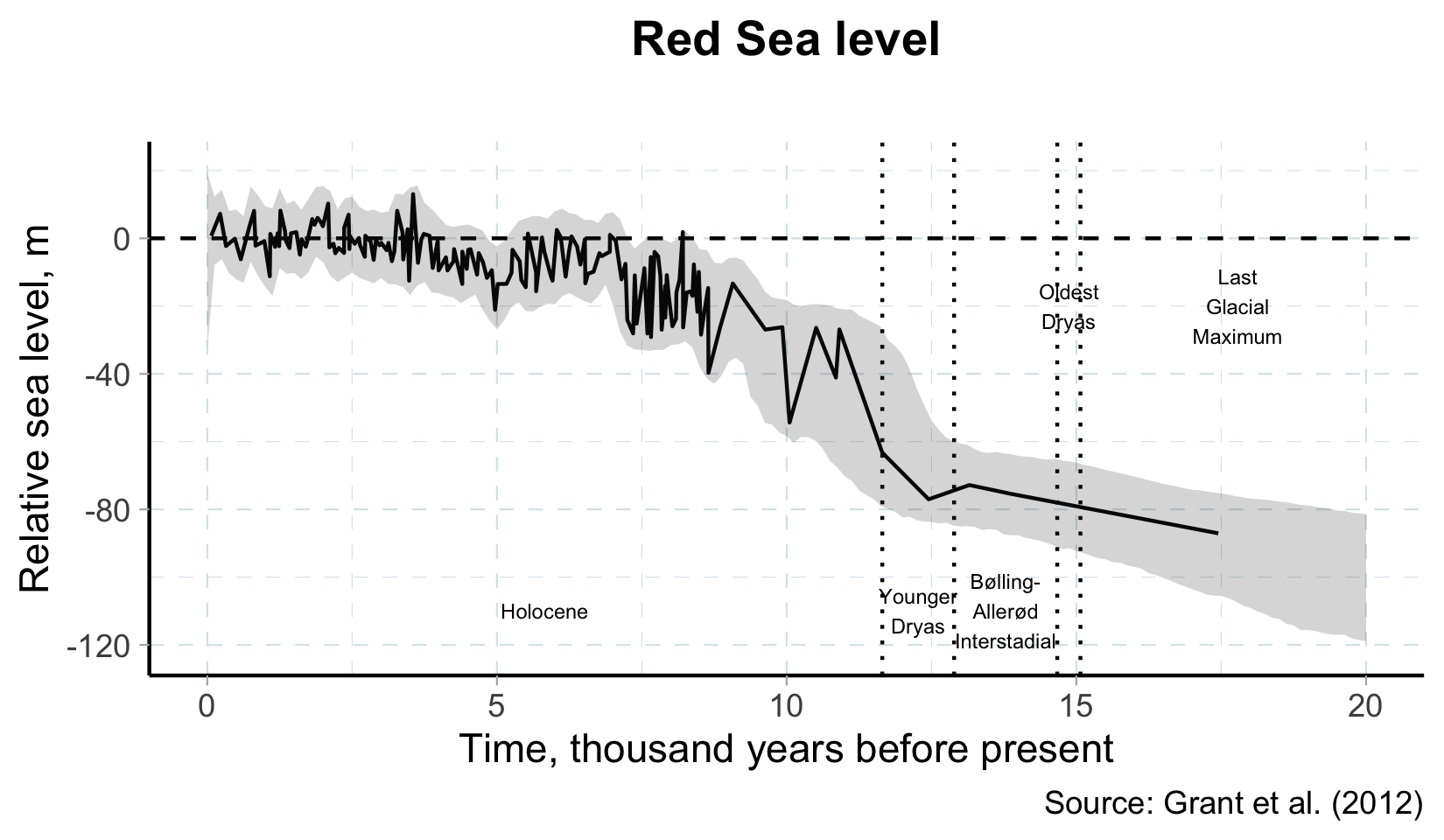
Climate and agriculture

Holocene (\(\approx\) 11,000 years ago - present)

  • warmer temperatures
  • increased precipitation
  • more stable climate (Feynman and Ruzmaikin 2007)

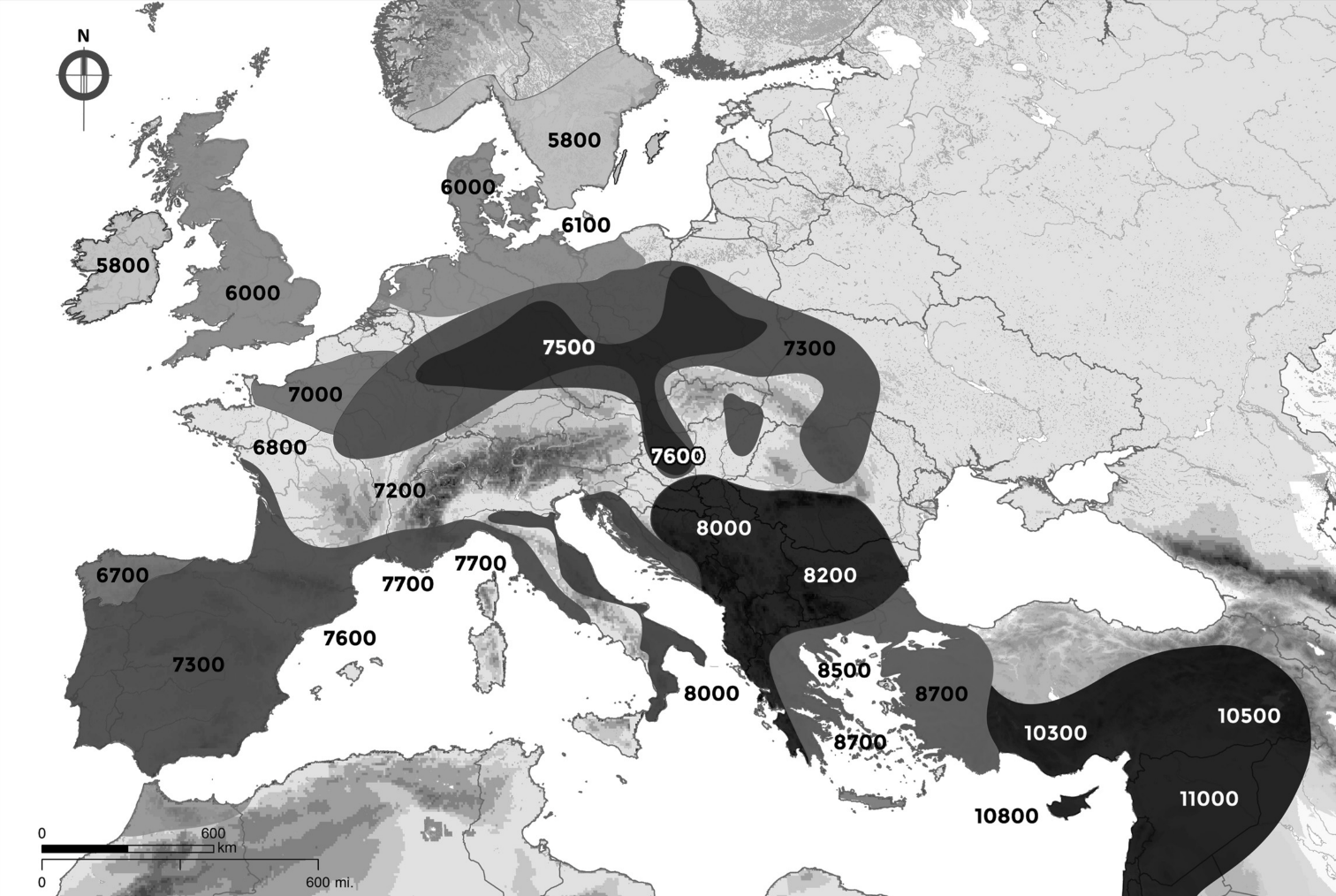
Agriculture

  • begins to spread \(\approx\) 11,000 years ago
  • higher marginal productivity thanks to climate change
  • evolutionary advantages: higher fertility, lower mortality (Shennan 2018)

Selection of farming-friendly genotypes

Model of genotype evolution

Based on Wright-Fisher model

  • finite, constant population \(N\)
  • \(K\) causal loci
  • unit of analysis - haplotype pairs \(\mathbf{H} = (l, r) = \left(\{0, 1\}^K, \{0, 1\}^K\right)\)
  • mutation, recombination, selection

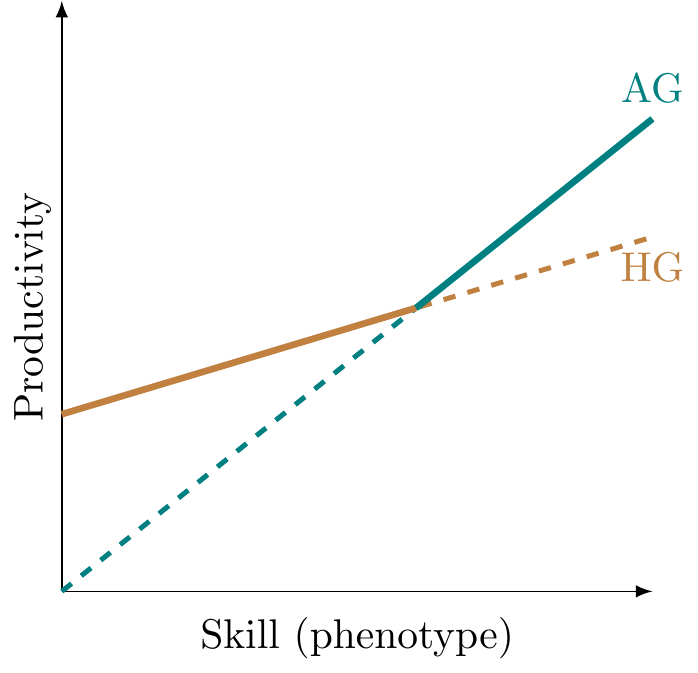
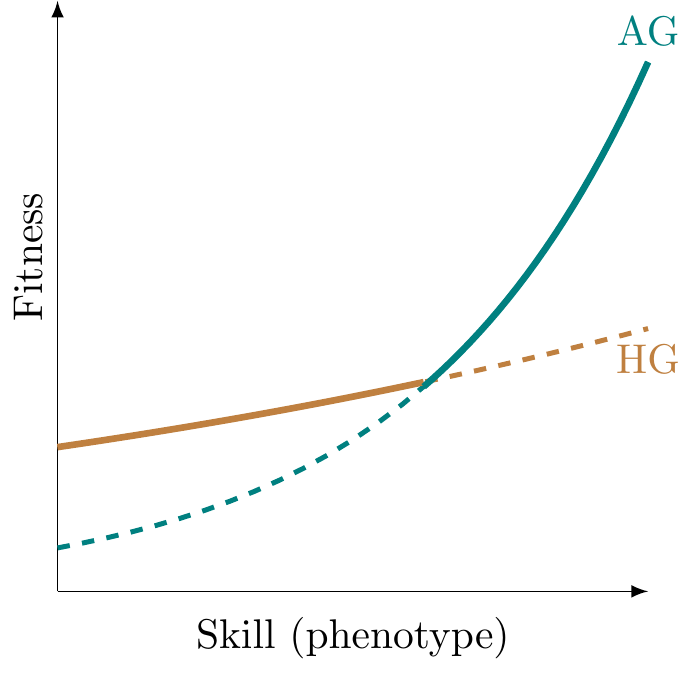
Selection and technology

  • \(z(g)\) is a polygenic score
    \[ z(g) = \sum_{k = 1}^K \beta(k) g(k) \]
  • two technologies: HG - foraging and AG - farming
  • technology-specific fitness function
    \[f(z, \tau) = R_\tau \exp\left(\omega_\tau z\right), \forall \tau \in \{HG, AG\}\]
  • fitness-maximising technology choice: \(\hat{f}(z) \equiv \max_\tau f(z, \tau)\)

Technology choice

Roy model

. . .

Adapted to fitness

Data

Genotypes

  • Ancient DNA (David Reich Lab 2021)
    • 2,328 unrelated ancient individuals from Western Eurasia
    • Allele frequencies in Western hunter-gatherer (WHG) population
  • 1000 Genome Project
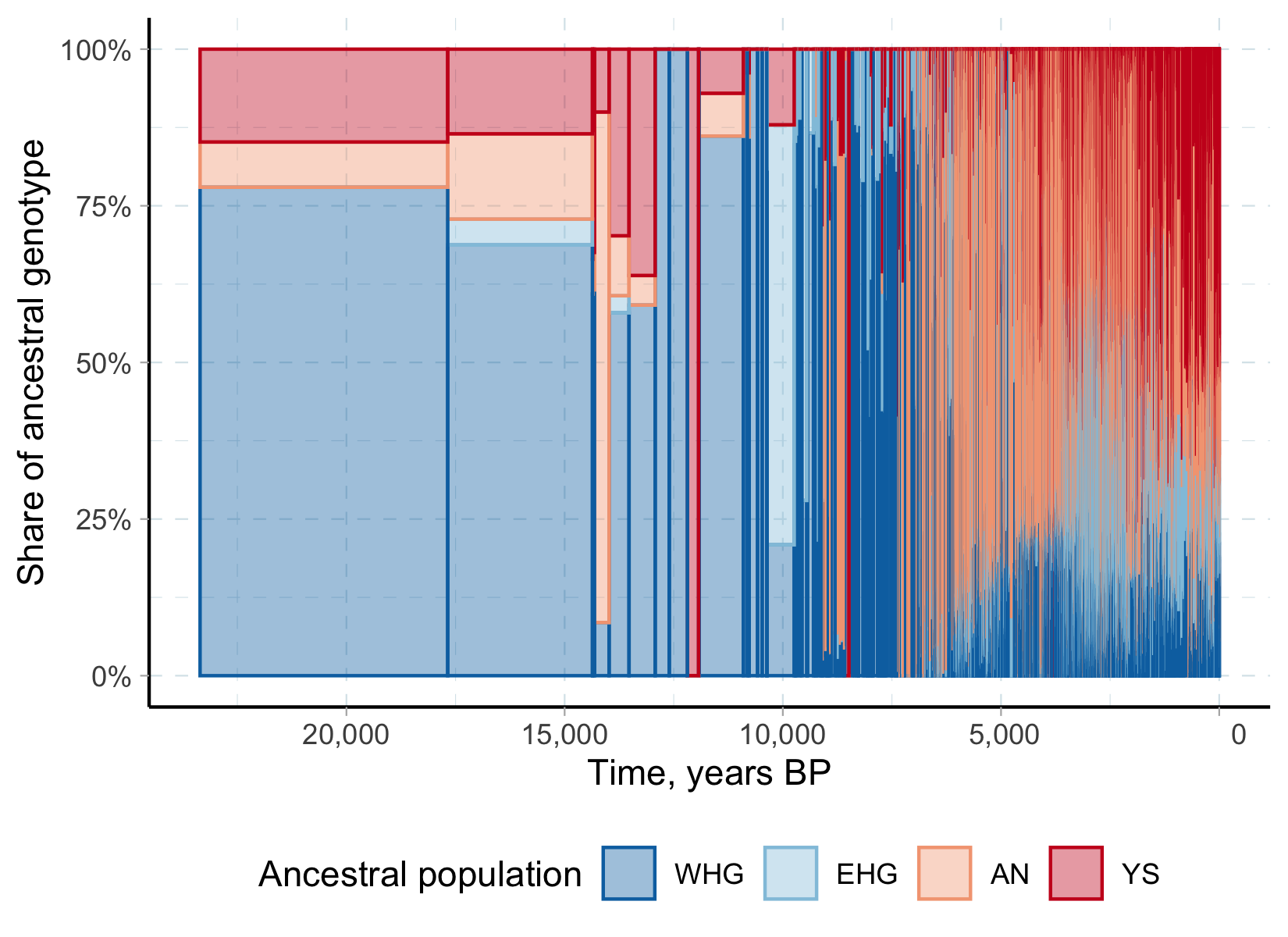
    • 503 individuals from EUR populations

GWAS estimates

  • Educational attainment (Lee et al. 2018)

Descriptive evidence

Education PGS in aDNA

Edge and Coop (2019) Waiting-time estimator

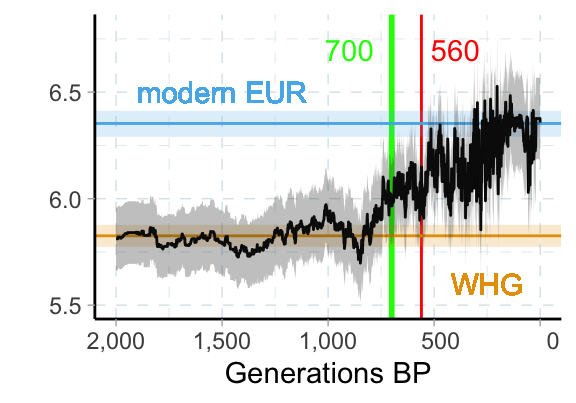
Estimation

Parameter of interest: technology-specific selection gradient \(\omega_\tau\)

  • Assume distribution before climate shift is at steady state: \(\omega_{HG} = 0\)
  • Estimate \(\omega_{AG}\) by maximising simulated likelihood

    • Draw initial haplotype matrix consistent with allele frequencies in WHG

    • Simulate independent histories from the model over \(T\) generations

    • Compute simulated likelihood of phenotypes in modern EUR

Results

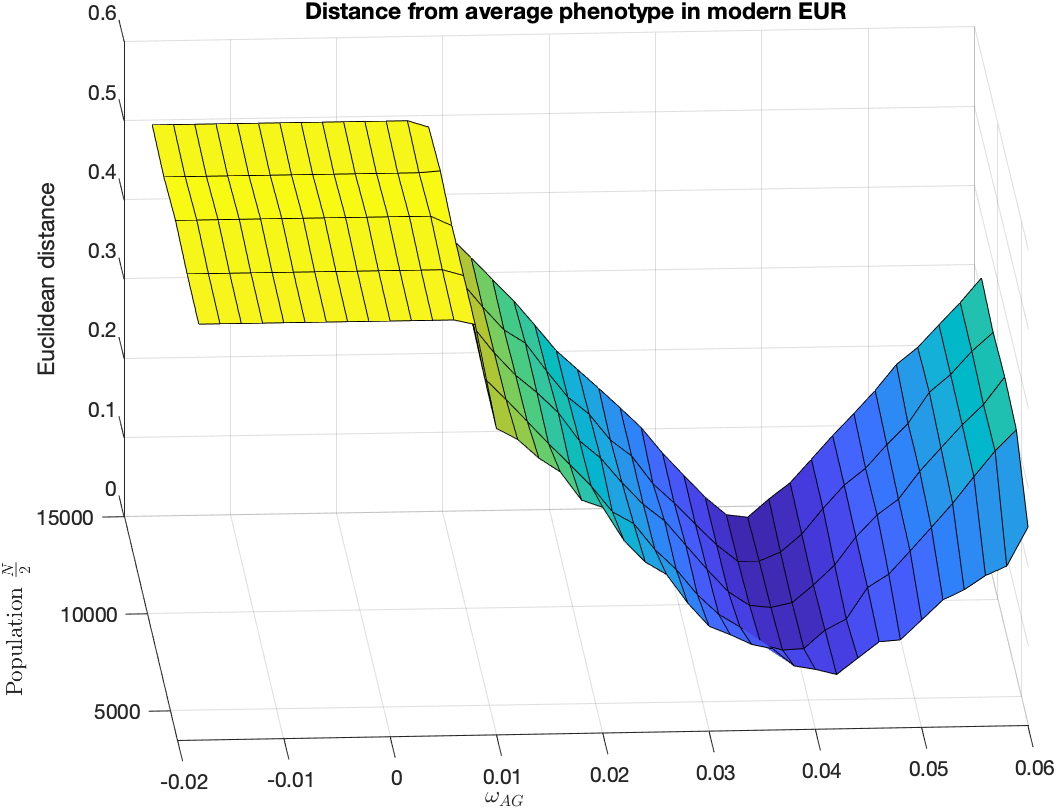
Results

Full sample

. . .

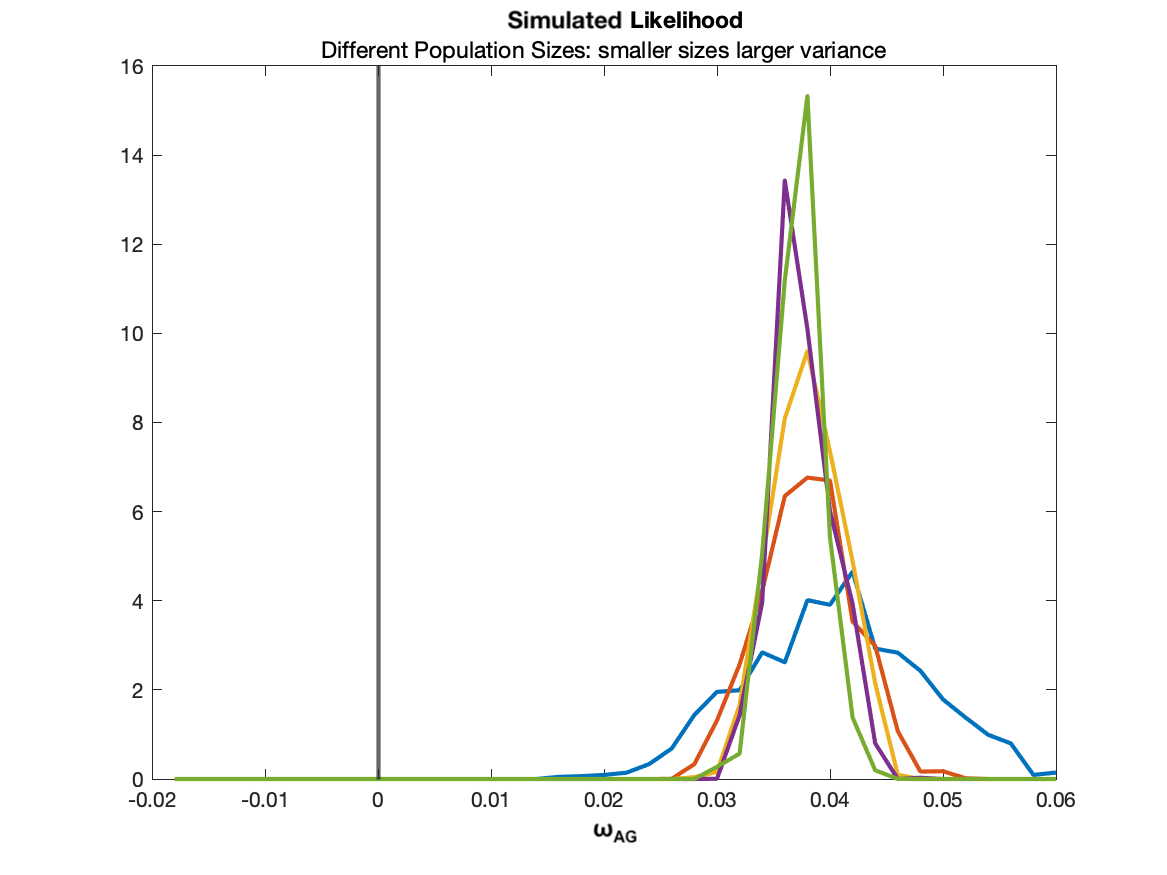
Truncated sample

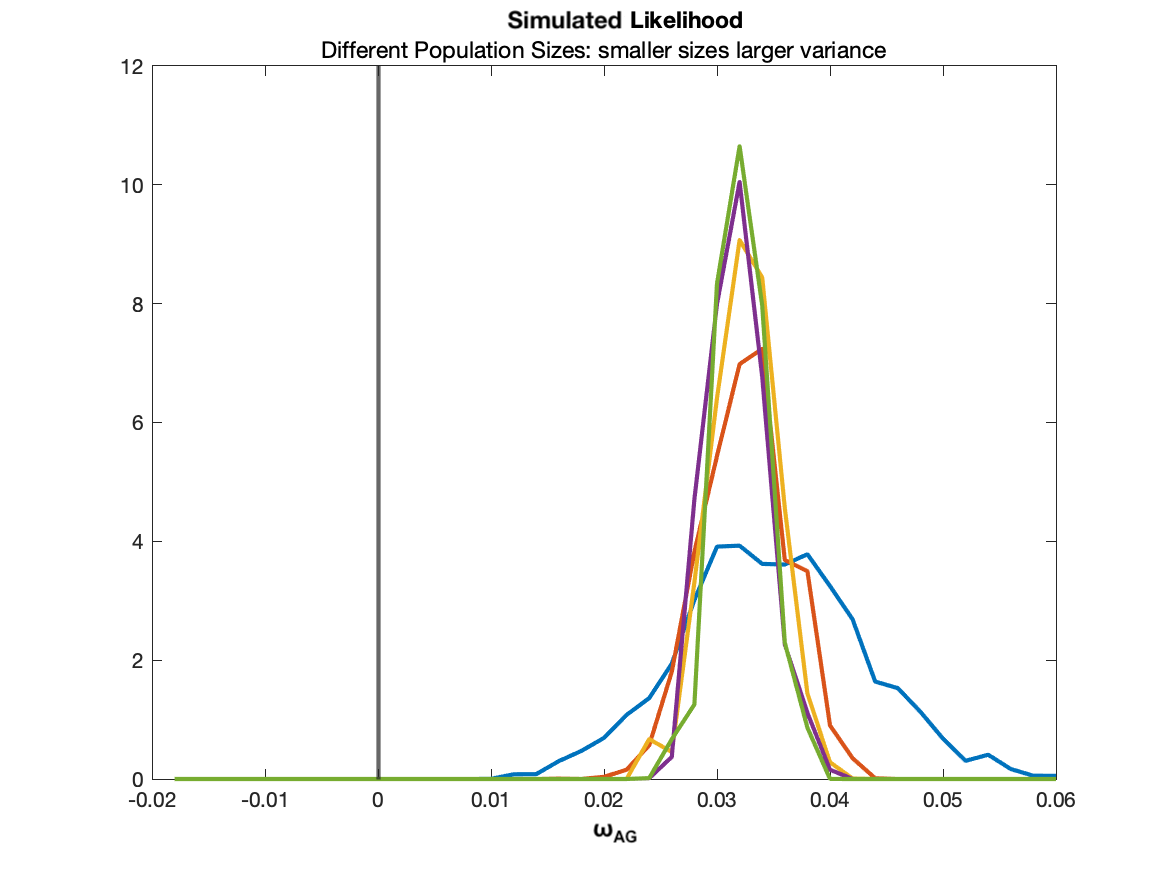
Conclusion

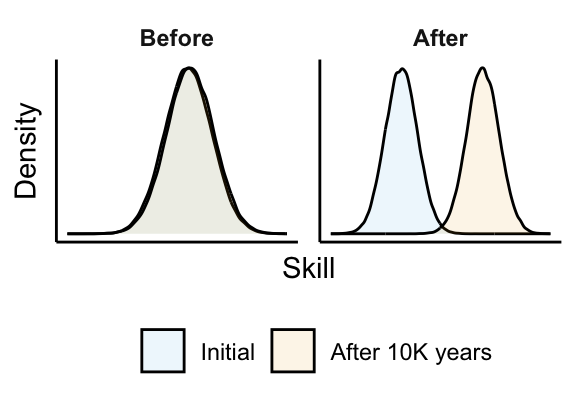
  • Study genetic evolution in European populations over the last 14,000 years
  • Extend Wright-Fisher model with activity choice in the spirit of Roy model
  • Estimate using ancient and modern genotypes

Future extensions:

  • Migration
  • Estimation with path

Climate (temperature)

Climate (precipitation)

Spread of farming

Reprinted Fig 1.1 from Shennan (2018). Dates are shown in years before present.

Process on haplotype pairs

  1. (Initial condition) Haplotype pairs \(h(t)\) at time \(t\)
  2. (Mutation) Random mutation, independent across alleles, loci and individuals.
  3. (Cross-over recombination) Non-homogeneous Poisson distribution
  4. (Random mating)
  5. (Reproduction) One haplotype from each parent, independently across children and chromosomes
  6. (Selection) Relative fitness of every child reaching the reproductive age
  7. (Next generation) Random draw from multinomial distribution over the haplotypes of size \(N\) and probabilities adjusted by the relative fitness

Climate shift and fitness

Fitness functions

Population distribution

Supervised ADMIXTURE