6. Technological shift and labour markets
KAT.TAL.322 Advanced Course in Labour Economics
April 3, 2024
Labour market of educated workers
Technological change and the labour market
Canonical model
Canonical model
Overview
Two types of labour: high- and low-skill
Typically, high edu and low edu (can be relaxed)Skill-biased technological change (SBTC)
New technology disproportionately \(\uparrow\) high-skill labour productivityHigh- and low-skill are imperfectly substitutable
Typically, CES production function with elasticity of substitution \(\sigma\)Competitive labour market
Canonical model
Production function
\[ Y = \left[\left(A_L L\right)^\frac{\sigma - 1}{\sigma} + \left(A_H H\right)^\frac{\sigma - 1}{\sigma}\right]^\frac{\sigma}{\sigma - 1} \]
\(A_L\) and \(A_H\) are factor-augmenting technology terms
\(\sigma \in [0, \infty)\) is the elasticity of substitution
- \(\sigma > 1\) gross substitutes
- \(\sigma < 1\) gross complements
- \(\sigma = 0\) perfect complements (Leontieff production)
- \(\sigma \rightarrow \infty\) perfect substitutes
- \(\sigma = 1\) Cobb-Douglas production
Canonical model
Interpretations
- There is only one good and \(H\) and \(L\) are imperfect substitutes in production
- There are two goods \(Y_H = A_H H\) and \(Y_L = A_L L\) and consumers have CES utility \(\left[Y_L^\frac{\sigma - 1}{\sigma} + Y_H^\frac{\sigma - 1}{\sigma}\right]^\frac{\sigma}{\sigma - 1}\)
- Combination of the two: different sectors produce goods that are imperfect substitutes and \(H\) and \(L\) are employed in both sectors.
Note
Supply of \(H\) and \(L\) is assumed inelastic \(\Rightarrow\) firm problem is sufficient.
Canonical model
Equilibrium wages
\[ \begin{align} w_L &= A_L^\frac{\sigma - 1}{\sigma} \left[A_L^\frac{\sigma - 1}{\sigma} + A_H^\frac{\sigma - 1}{\sigma}\left(\frac{H}{L}\right)^\frac{\sigma - 1}{\sigma}\right]^\frac{1}{\sigma - 1}\\ w_H &= A_H^\frac{\sigma - 1}{\sigma} \left[A_L^\frac{\sigma - 1}{\sigma}\left(\frac{H}{L}\right)^{-\frac{\sigma - 1}{\sigma}} + A_H^\frac{\sigma - 1}{\sigma}\right]^\frac{1}{\sigma - 1} \end{align} \]
Comparative statics:
\(\frac{\partial w_L}{\partial H/L} > 0\) low-skill wage rises with \(\frac{H}{L}\)
\(\frac{\partial w_H}{\partial H/L} < 0\) high-skill wage falls with \(\frac{H}{L}\)
\(\frac{\partial w_i}{\partial A_L} > 0\) and \(\frac{\partial w_i}{\partial A_H} > 0, ~\forall i \in \{L, H\}\) both wages rise with \(A_L\) and \(A_H\)
Canonical model
Skill premium
\[ \frac{w_H}{w_L} = \left(\frac{A_H}{A_L}\right)^\frac{\sigma - 1}{\sigma} \left(\frac{H}{L}\right)^{-\frac{1}{\sigma}} \]
\(\Delta\) relative supply
\[ \frac{\partial \ln \frac{w_H}{w_L}}{\partial \ln \frac{H}{L}} = -\frac{1}{\sigma} < 0 \]
Relative demand curve is downward-sloping
\(\Delta\) technology
\[ \frac{\partial \ln\frac{w_H}{w_L}}{\partial \ln\frac{A_H}{A_L}} = \frac{\sigma - 1}{\sigma} \lessgtr 0 \]
- Gross substitutes: \(\sigma > 1 \Rightarrow \frac{\partial \ln w_H/ w_L}{\partial \ln A_H / A_L} > 0\)
- Gross complements: \(\sigma < 1 \Rightarrow \frac{\partial \ln w_H/ w_L}{\partial \ln A_H / A_L} < 0\)
- Cobb-Douglas: \(\sigma = 1 \Rightarrow \frac{\partial \ln w_H/ w_L}{\partial \ln A_H / A_L} = 0\)
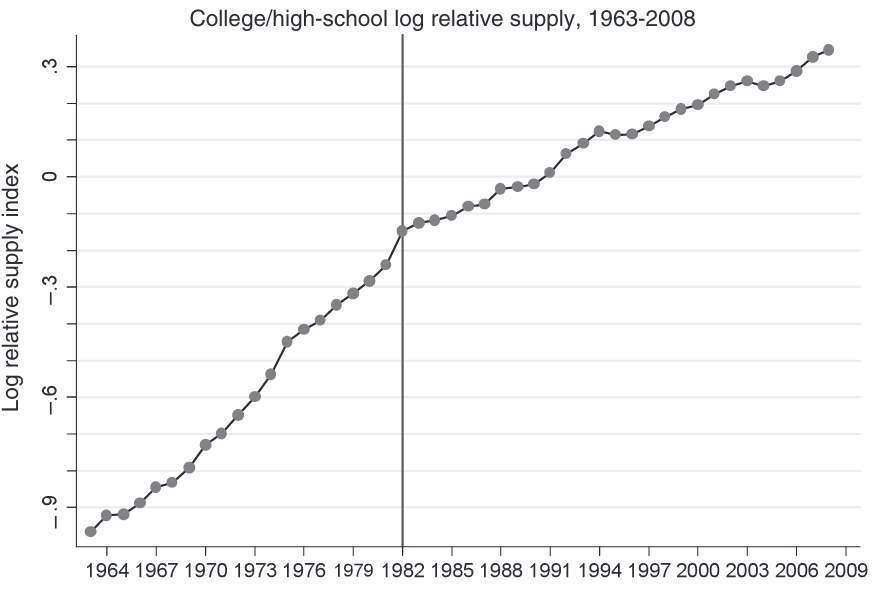
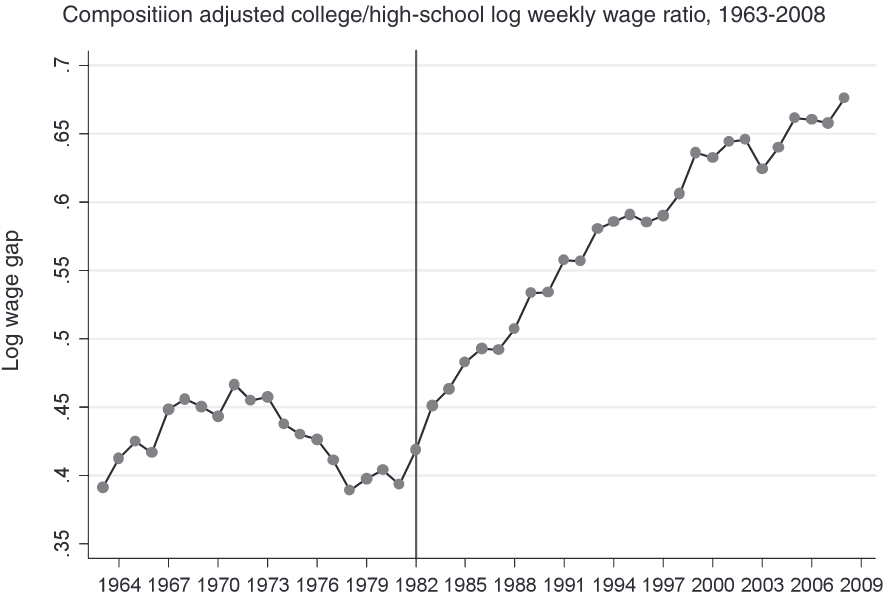
Tinbergen’s race in the data
Katz and Murphy (1992)
The log-equation of skill premium is extremely attractive for empirical analysis
\[ \ln\frac{w_{H, t}}{w_{L, t}} = \frac{\sigma - 1}{\sigma} \ln\left(\frac{A_{H, t}}{A_{L, t}}\right) -\frac{1}{\sigma} \ln \left(\frac{H_t}{L_t}\right) \]
Assume a log-linear trend in relative productivities
\[ \ln \left(\frac{A_{H, t}}{A_{L, t}}\right) = \alpha_0 + \alpha_1 t \]
and plug it into the log skill premium equation:
\[ \ln\frac{w_{H, t}}{w_{L, t}} = \frac{\sigma - 1}{\sigma}\alpha_0 + \frac{\sigma - 1}{\sigma} \alpha_1 t -\frac{1}{\sigma} \ln\left(\frac{H_t}{L_t}\right) \]
Tinbergen’s race in the data
Katz and Murphy (1992)
Estimated the skill premium equation using the US data in 1963-87
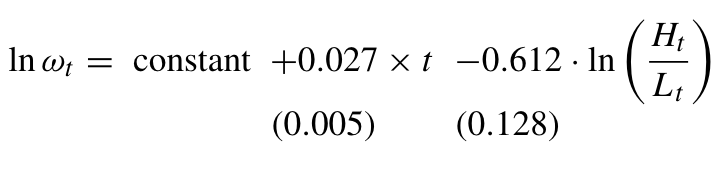
Implies elasticity of substitution \(\sigma \approx \frac{1}{0.612} =\) 1.63
Agrees with other estimates that place \(\sigma\) between 1.4 and 2 (Acemoglu and Autor 2011)
Tinbergen’s race in the data
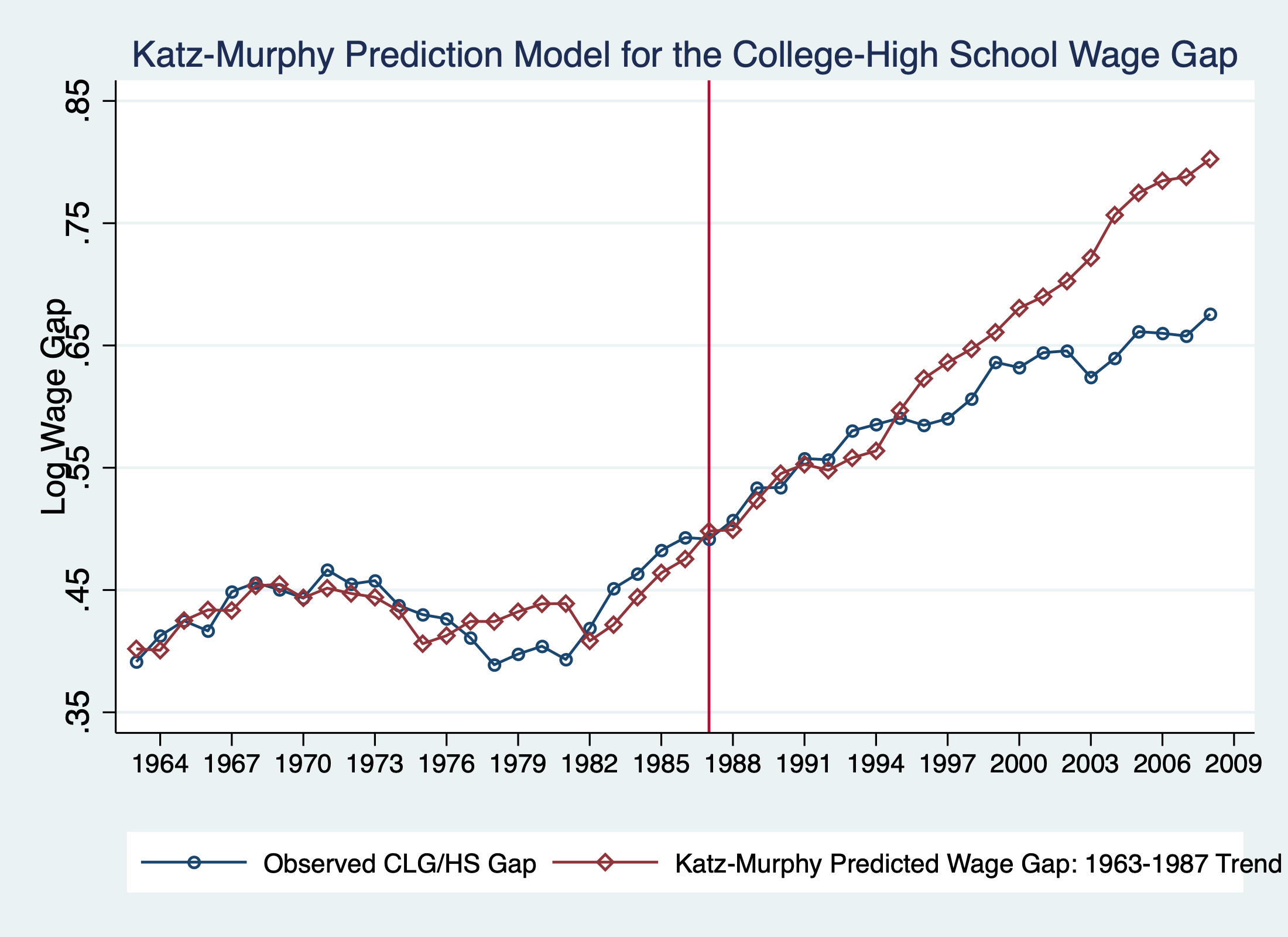
Very close fit up to mid-1990s, diverge later
Fit up to 2008 implies \(\sigma \approx\) 2.95
Accounting for divergence:
non-linear time trend in \(\ln\frac{A_H}{A_L}\)
brings \(\sigma\) back to 1.8, but implies \(\frac{A_H}{A_L}\) slowed downdifferentiate labour by age/experience as well
Canonical model
Summary
- Simple link between wage structure and technological change
- Attractive explanation for college/no college wage inequality1
- Average wages \(\uparrow\) (follows from \(\partial w_i / \partial A_H\) and \(\partial w_i/ \partial A_L\))
However, the model cannot explain other trends observed in the data:
- Falling \(w_L\)
- Earnings polarization
- Job polarization
Also silent about endogeneous adoption or labour-replacing technology.
Unexplained trend: falling real wages
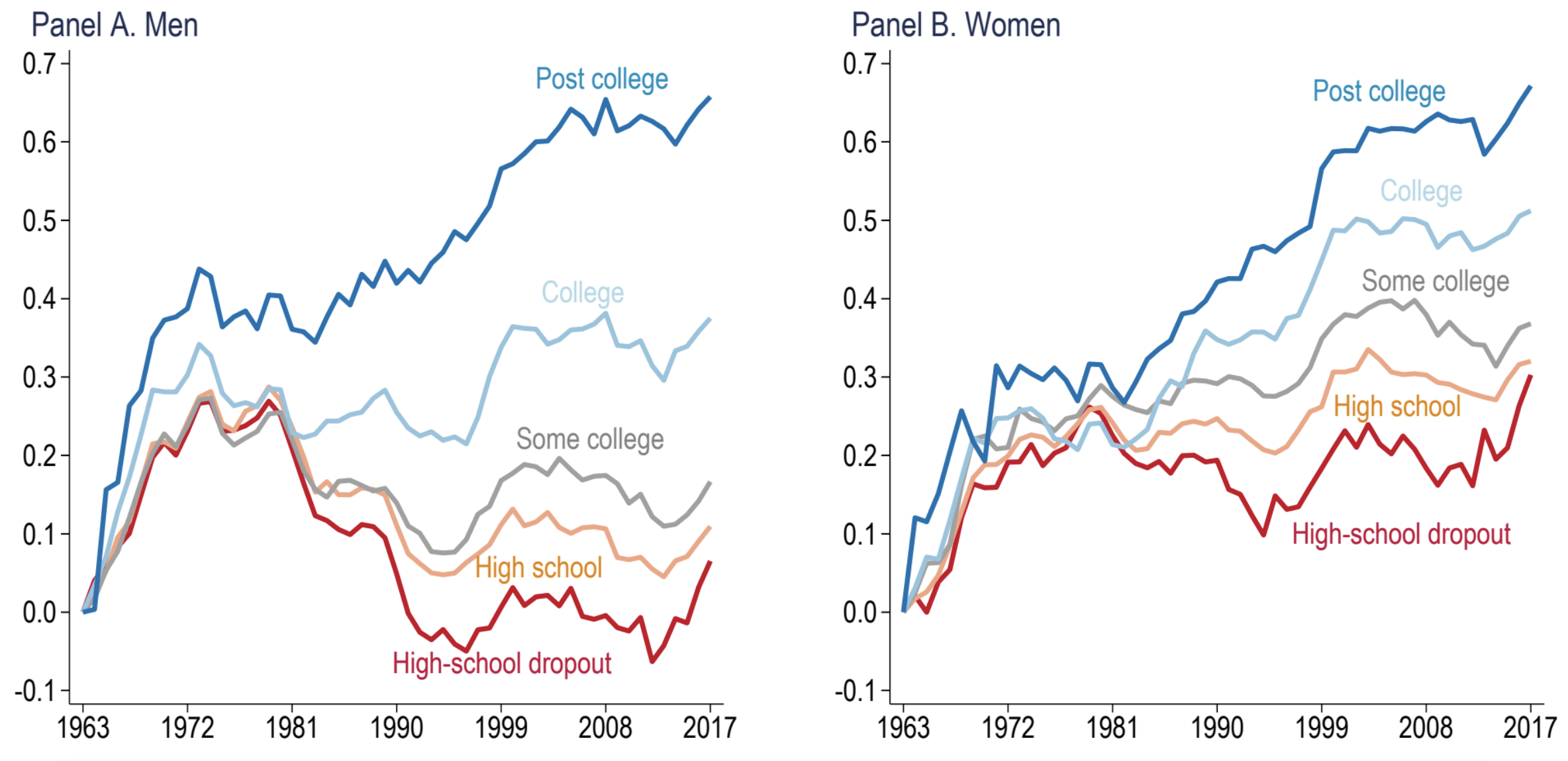
Source: Figure 1 in Acemoglu and Restrepo (2022)
Unexplained trend: earnings polarization
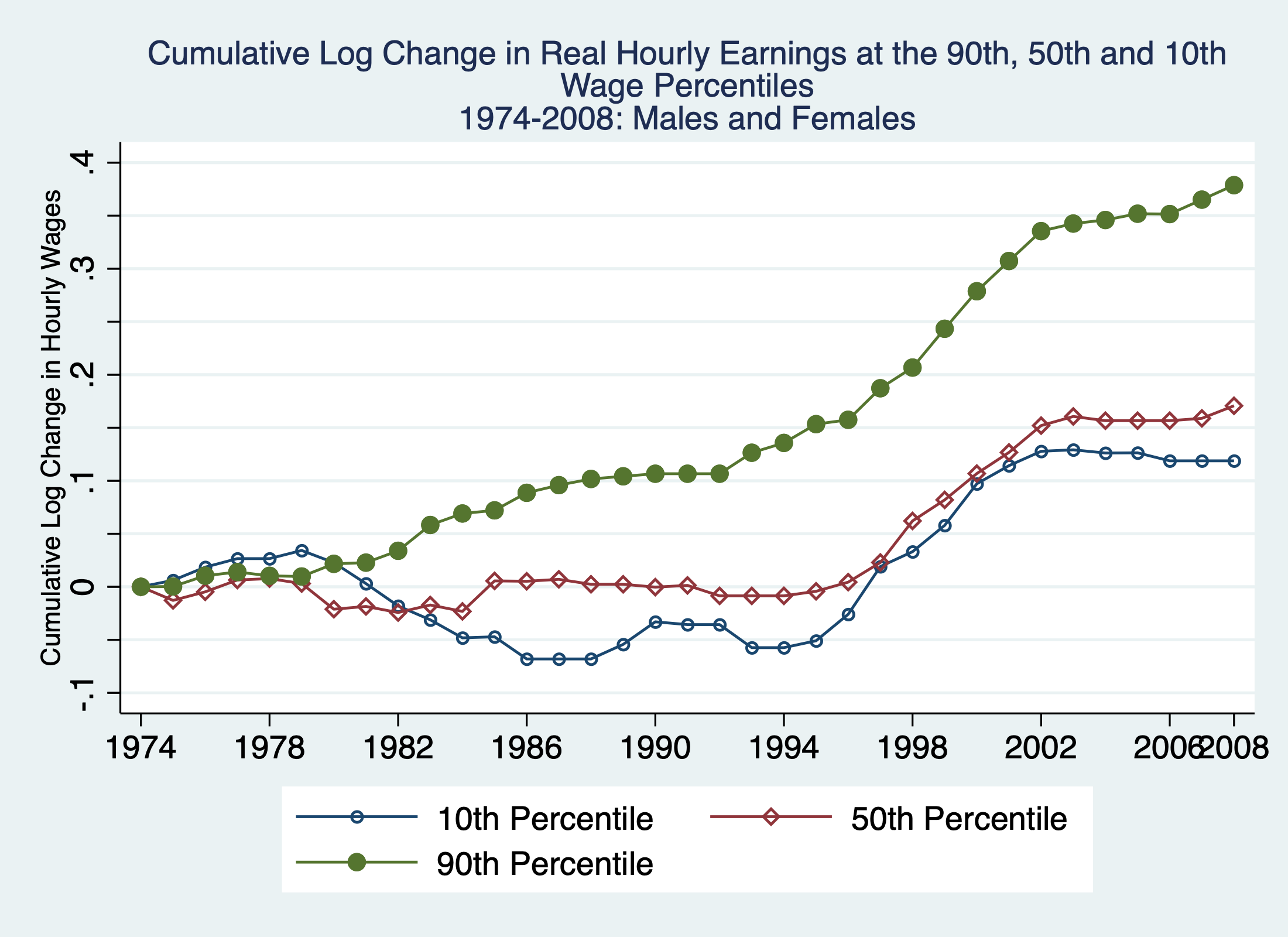
Source: Figure 8 in Acemoglu and Autor (2011)
Unexplained trend: job polarization
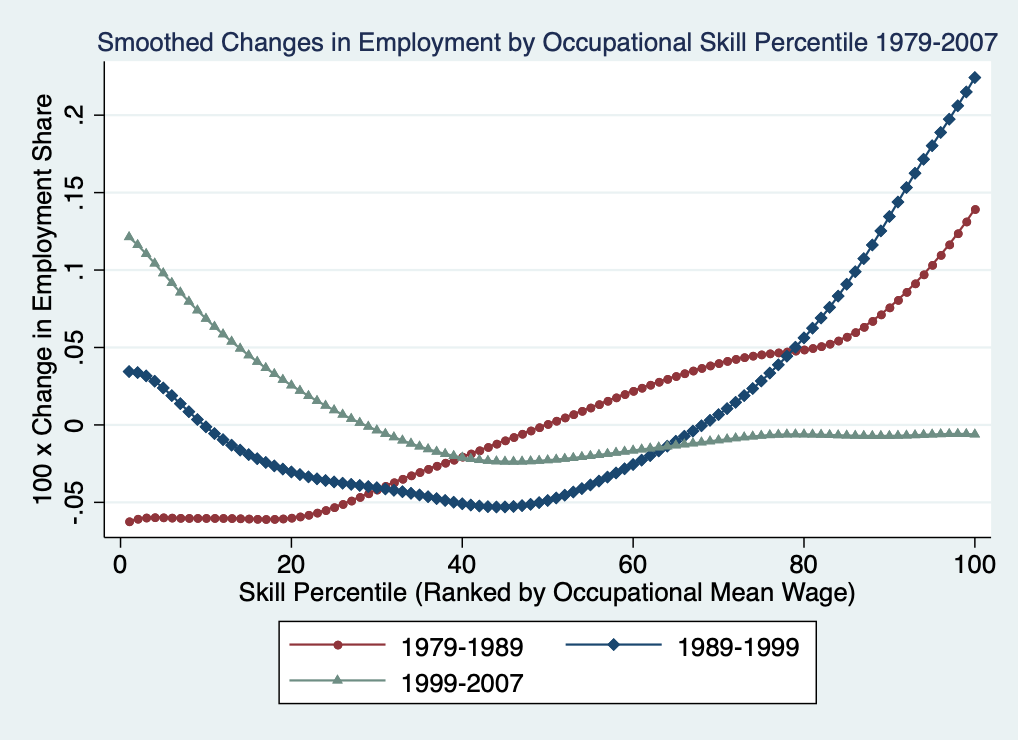
Source: Figure 10 in Acemoglu and Autor (2011)
Task-based model
Task-based model
Overview
Task is a unit of work activity that produces output
Skill is a worker’s endowment of capabilities for performing tasks
Key features:
- Tasks can be performed by various inputs (skills, machines)
- Comparative advantage over tasks among workers
- Multiple skill groups
- Consistent with canonical model predictions
Task-based model
Production function
Unique final good \(Y\) produced by continuum of tasks \(i \in [0, 1]\)
\[ Y = \exp \left[\int_0^1 \ln y(i) \text{d}i\right] \]
Three types of labour: \(H\), \(M\) and \(L\) supplied inelastically.
\[ y(i) = A_L \alpha_L(i) l(i) + A_M \alpha_M(i) m(i) + A_H \alpha_H(i) h(i) + A_K \alpha_K(i) k(i) \]
\(A_L, A_M, A_H\) are factor-augmenting technologies
\(\alpha_L(i), \alpha_M(i), \alpha_H(i)\) are task productivity schedules
\(l(i), m(i), h(i)\) are number of workers by types allocated to task \(i\)
Task-based model
Comparative advantage assumption
\(\alpha_L(i)/\alpha_M(i)\) and \(\alpha_M(i)/\alpha_H(i)\) are continuously differentiable and strictly decreasing.
Market clearing conditions
\[ \int_0^1 l(i) \text{d}i \leq L \qquad \int_0^1 m(i) \text{d}i \leq M \qquad \int_0^1 h(i) \text{d}i \leq H \]
Task-based model
Equilibrium without machines
Lemma 1
Given comparative advantage assumption, there exist \(I_L\) and \(I_H\) such that
Note that boundaries \(I_L\) and \(I_H\) are endogenous
This gives rise to the substitution of skills across tasks
Task-based model
Law of one wage
Output price is normalised to 1 \(\Rightarrow \exp\left[\int_0^1 \ln p(i) \text{d}i\right] = 1\)
All tasks employing a given skill pay corresponding wage
\[ \begin{align} w_L &= \frac{A_L \alpha_L(i)}{p(i)} &\Rightarrow& \qquad l(i) &=& \frac{L}{I_L} &\forall& i < I_L \\ w_M &= \frac{A_M \alpha_M(i)}{p(i)} &\Rightarrow& \qquad m(i) &=& \frac{M}{I_H - I_L} &\forall& I_L < i < I_H \\ w_H &= \frac{A_H \alpha_H(i)}{p(i)} &\Rightarrow& \qquad h(i) &=& \frac{H}{1 - I_H} &\forall& i > I_H \end{align} \]
Task-based model
Endogenous thresholds: no arbitrage
Threshold task \(I_H\): equally profitable to produce with either \(H\) or \(M\) skills
\[ \frac{A_M \alpha_M(I_H) M}{I_H - I_L} = \frac{A_H \alpha_H(I_H) H}{1 - I_H} \]
Similarly, for \(I_L\):
\[ \frac{A_L \alpha_L(I_L) L}{I_L} = \frac{A_M \alpha_M(I_L) M}{I_H - I_L} \]
Task-based model
Endogenous thresholds: no arbitrage
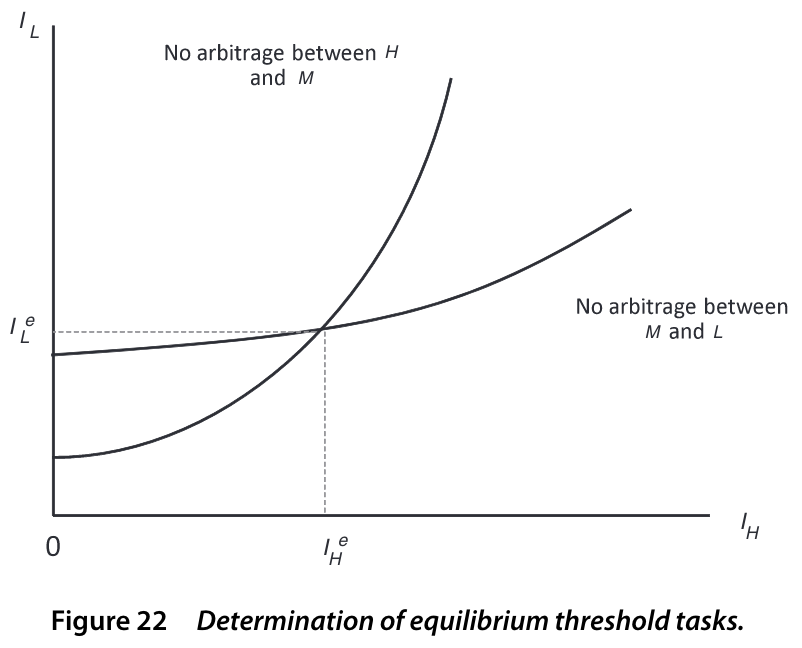
Task-based model
Comparative statics: wage elasticities
\[ \begin{matrix} \frac{\text{d} \ln w_H / w_L}{\text{d}\ln A_H} > 0 & \frac{\text{d} \ln w_M / w_L}{\text{d}\ln A_H} < 0 & \frac{\text{d} \ln w_H / w_M}{\text{d}\ln A_H} > 0 \\ \frac{\text{d} \ln w_H / w_L}{\text{d}\ln A_M} \lesseqqgtr 0 & \frac{\text{d} \ln w_M / w_L}{\text{d}\ln A_M} > 0 & \frac{\text{d} \ln w_H / w_M}{\text{d}\ln A_M} < 0 \\ \frac{\text{d} \ln w_H / w_L}{\text{d}\ln A_L} < 0 & \frac{\text{d} \ln w_M / w_L}{\text{d}\ln A_L} < 0 & \frac{\text{d} \ln w_H / w_M}{\text{d}\ln A_L} > 0 \end{matrix} \]
Consider \(\uparrow A_M\):
- \(M\) more productive \(\Rightarrow ~ \uparrow\) set of medium-skill tasks \(\uparrow I_H\) and/or \(\downarrow I_L\)
- Since supply is constant, \(\uparrow w_M\) and \(\downarrow w_H, w_L\)
- Depending on comparative advantages:
- \(\left|\beta^\prime_L(I_L) I_L\right| > \left|\beta^\prime_H(I_H)(1 - I_H)\right| \Rightarrow \frac{w_H}{w_L} \downarrow\)
- \(\left|\beta^\prime_L(I_L) I_L\right| < \left|\beta^\prime_H(I_H)(1 - I_H)\right| \Rightarrow \frac{w_H}{w_L} \uparrow\)
Task-based model
Task replacing technologies
Assume in \([\underline{I}, \bar{I}] \subset [I_L, I_H]\) machines outperform \(M\)1. Otherwise, \(\alpha_K(i) = 0\).
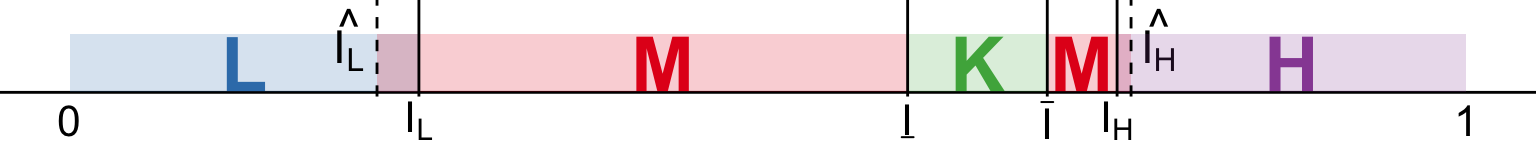
In this case,
- \(w_H / w_M\) increases
- \(w_M / w_L\) decreases
- \(w_H / w_L \uparrow \color{#9a2515}{\left(\downarrow\right)}\) if \(\left|\beta^\prime_L(I_L) I_L\right| \stackrel{<}{\color{#9a2515}{>}} \left|\beta^\prime_H(I_H)(1 - I_H)\right|\)
Task-based model
Endogenous supply of skills
Each worker \(j\) is endowed with some amount of each skill \(l^j, m^j, h^j\)
Workers allocate time to each skill given
\[ \begin{align} &t_l^j + t_m^j + t_h^j \leq 1 \\ &w_L t_l^j l^j + w_M t_m^j m^j + w_H t_h^j h^j \end{align} \]
Assuming that \(\frac{h^j}{m^j}\) and \(\frac{m^j}{l^j}\) are decreasing in \(j\), there exist \(J^\star\left(\frac{w_H}{w_M}\right)\) and \(J^{\star\star}\left(\frac{w_M}{w_L}\right)\)

Task-based model
Illustration in the data
Suppose \(A_H \uparrow\). The model predicts that \(\frac{w_H}{w_M} \uparrow\) and \(\frac{w_M}{w_L} \downarrow\).
Use occupational specialization at some \(t = 0\) as comparative advantage.
- \(\gamma_{sejk}^i\) share of 1959 population employed in \(i\) occupations, \(\forall i \in \{H, M, L\}\)
\[ \Delta w_{sejk\tau} = \sum_t \left[\beta_t^H \gamma_{sejk}^H + \beta_t^L \gamma_{sejk}^L\right] 1\{\tau = t\} + \delta_\tau + \phi_e + \lambda_j + \pi_k + e_{sejk\tau} \]
Descriptive regression informed by the model!
Task-based model
Illustration in the data
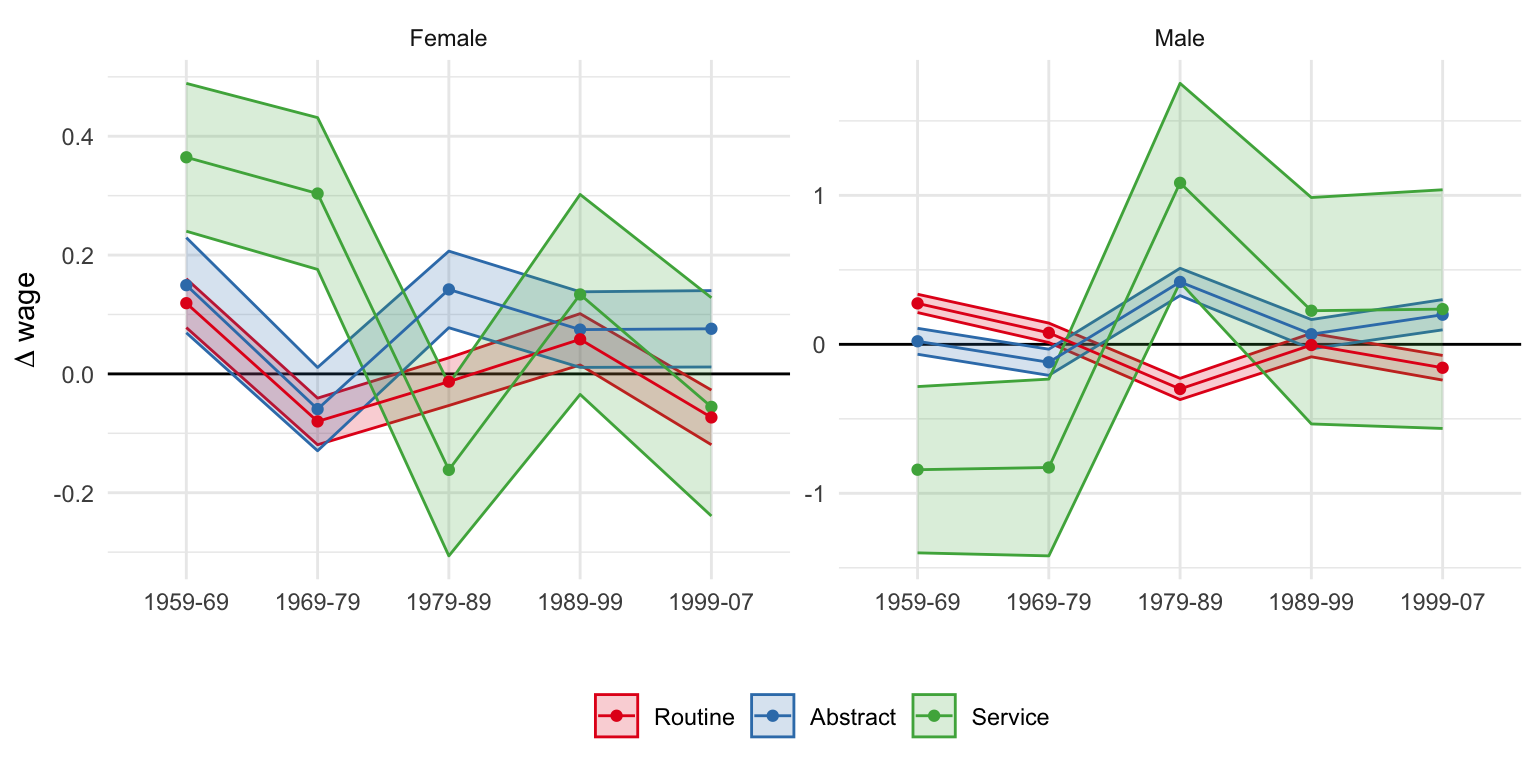
Source: Table 10 in Acemoglu and Autor (2011)
Task-based model
Summary
- A rich model that can accommodate numerous scenarios
- Outsourcing tasks to lower-cost countries
- Endogenous technological change
- Creation of new tasks
- Useful tool to study effect on inequality and job polarization
Empirical results
Acemoglu and Restrepo (2022)
Environment
Multi-sector model with imperfect substitution between production inputs
\[ \text{Task displacement}_g^\text{direct} = \sum_{i \in \mathcal{I}} \omega_g^i \frac{\omega_{gi}^R}{\omega_i^R} \left(-d \ln s_i^{L, \text{auto}}\right) \]
\(\omega_g^i\) - share of wages earned by worker group \(g\) in industry \(i\)
(exposure to industry \(i\))\(\frac{\omega_{gi}^R}{\omega_i^R}\) - specialization of group \(g\) in routine tasks \(R\) within industry \(i\)
\(-d \ln s_i^{L, \text{auto}}\) - % decline in industry \(i\)’s labour share due to automation
attribute 100% of the decline to automation
predict given industry adoption of automation technology
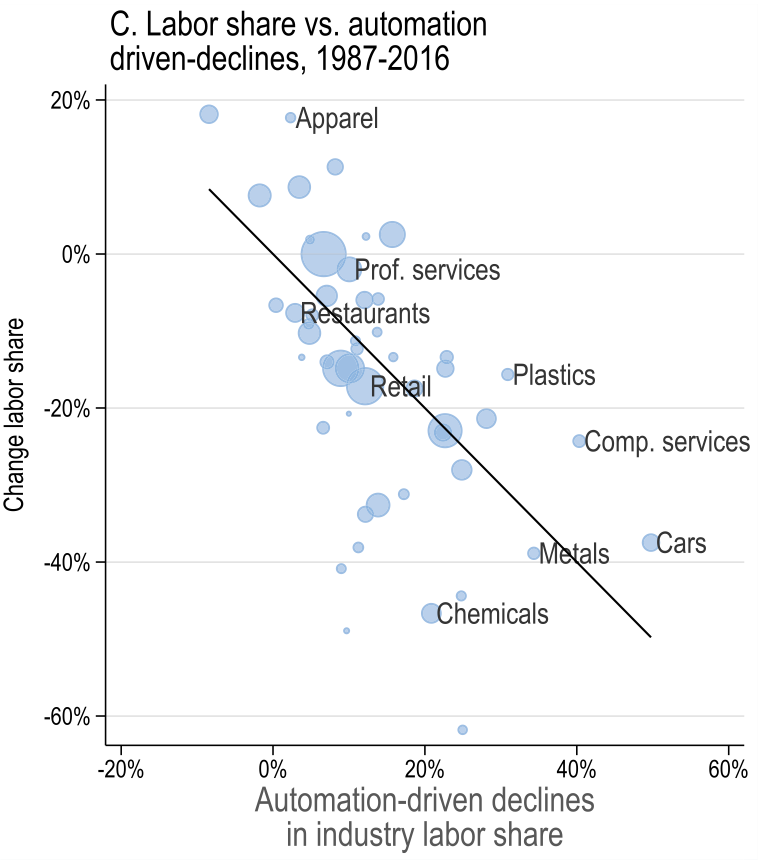
Acemoglu and Restrepo (2022)
Task displacement
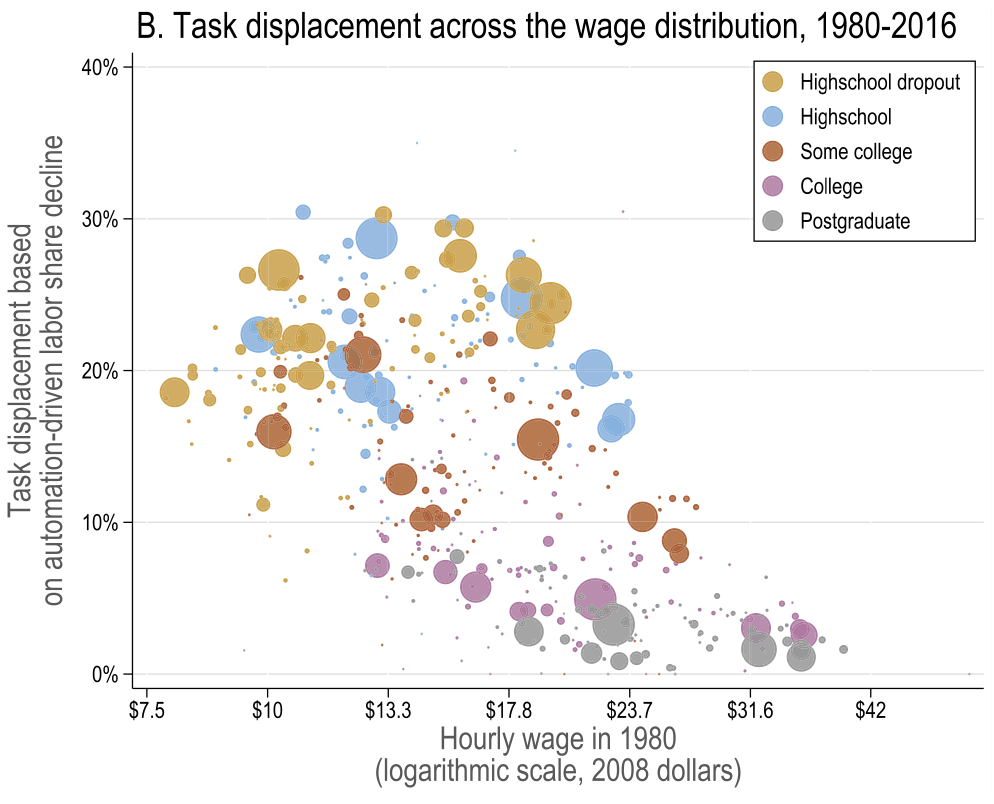
Source: Figure 5
Acemoglu and Restrepo (2022)
Task displacement and changes in real wages
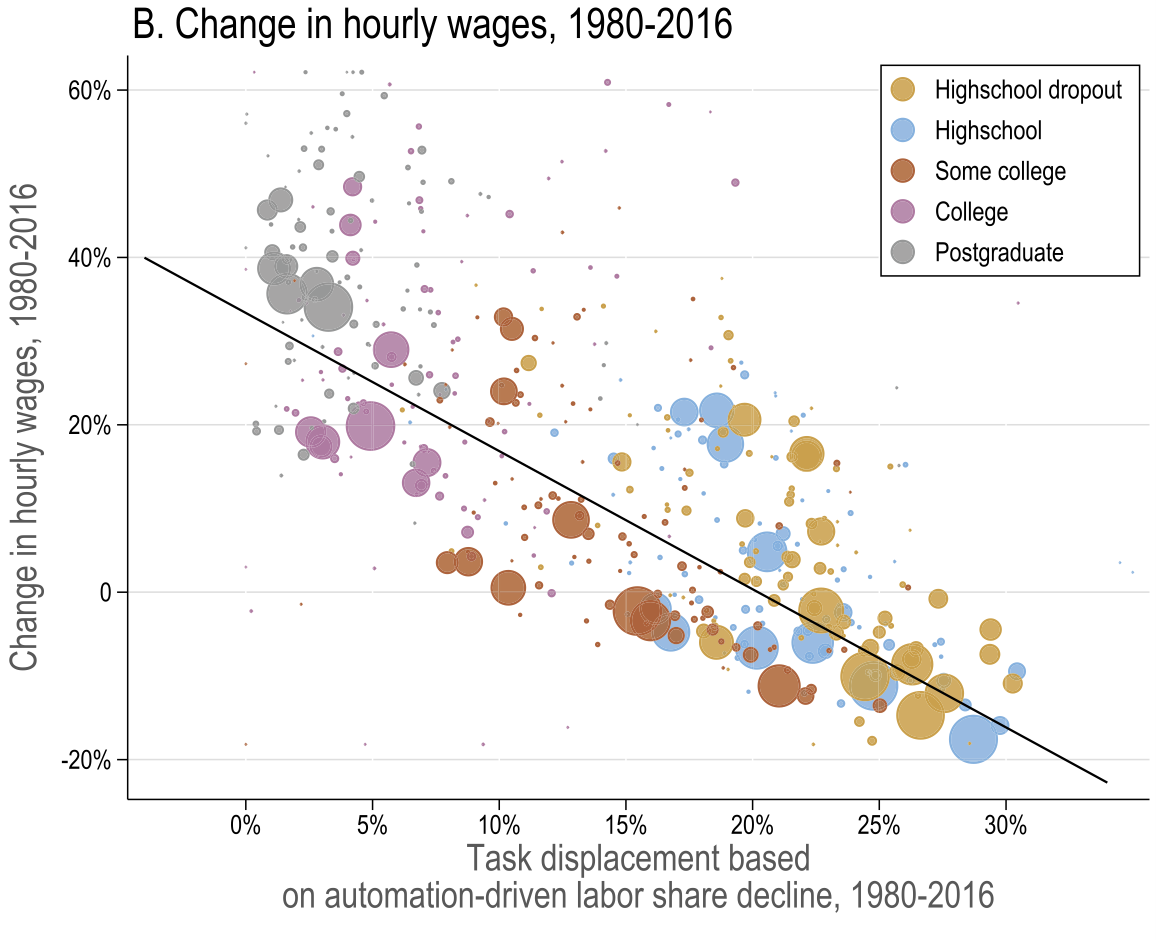
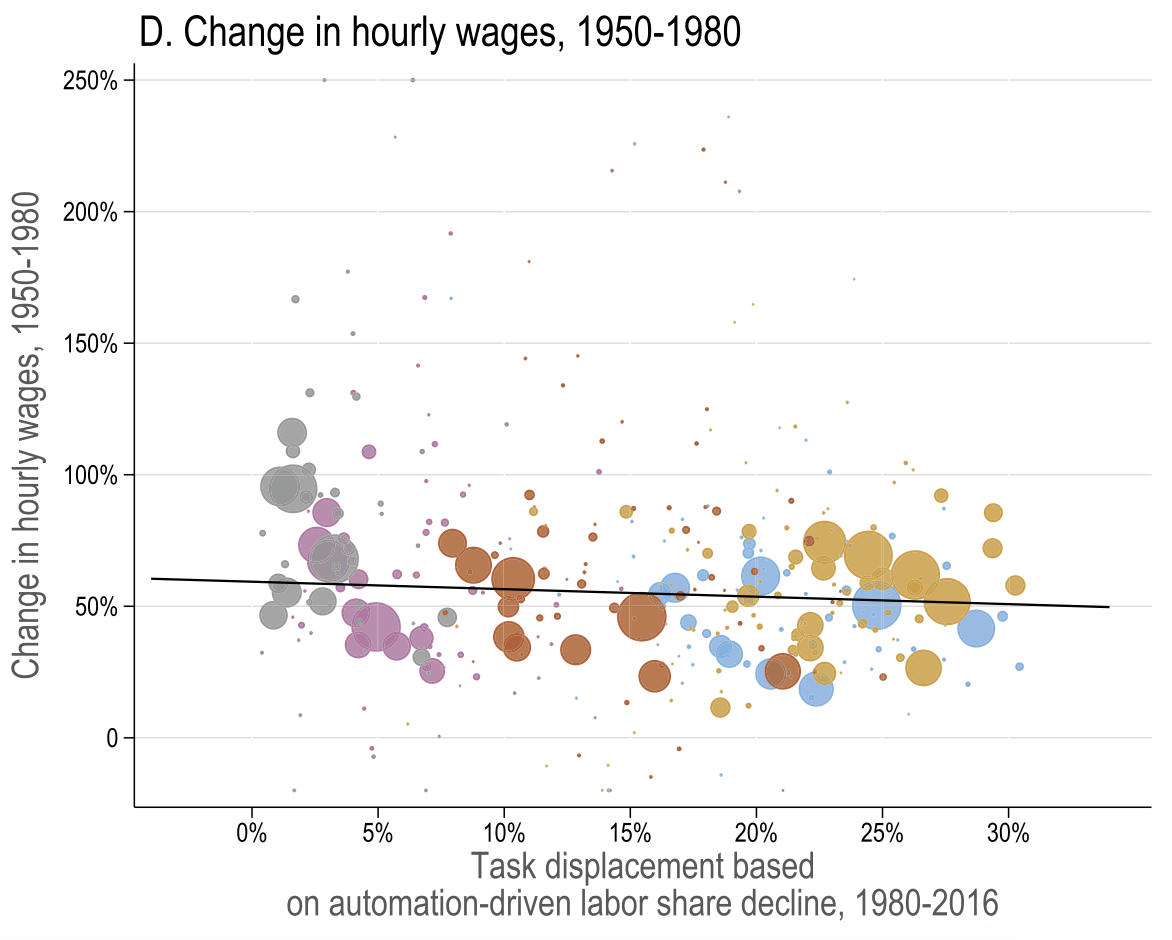
Acemoglu and Restrepo (2022)
General equilibrium results
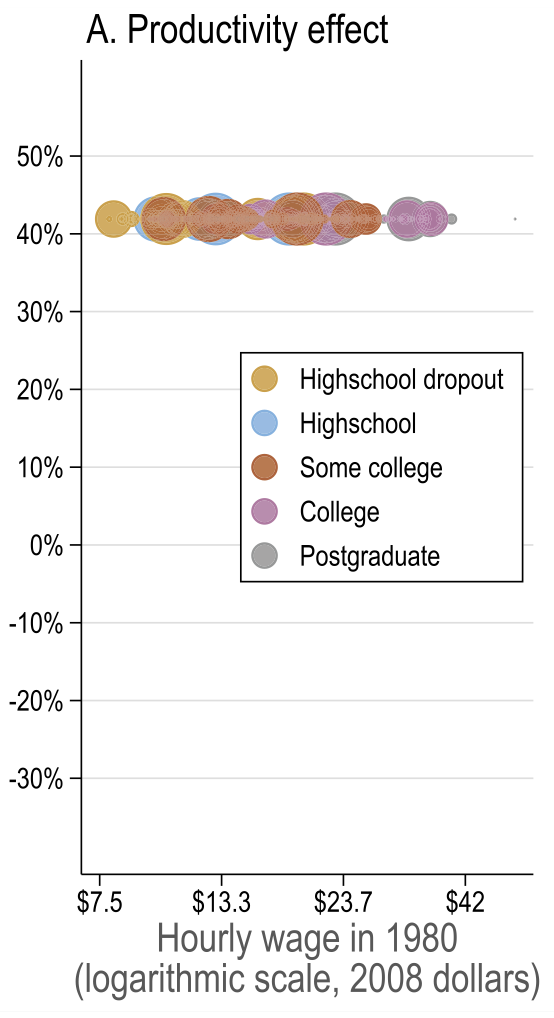
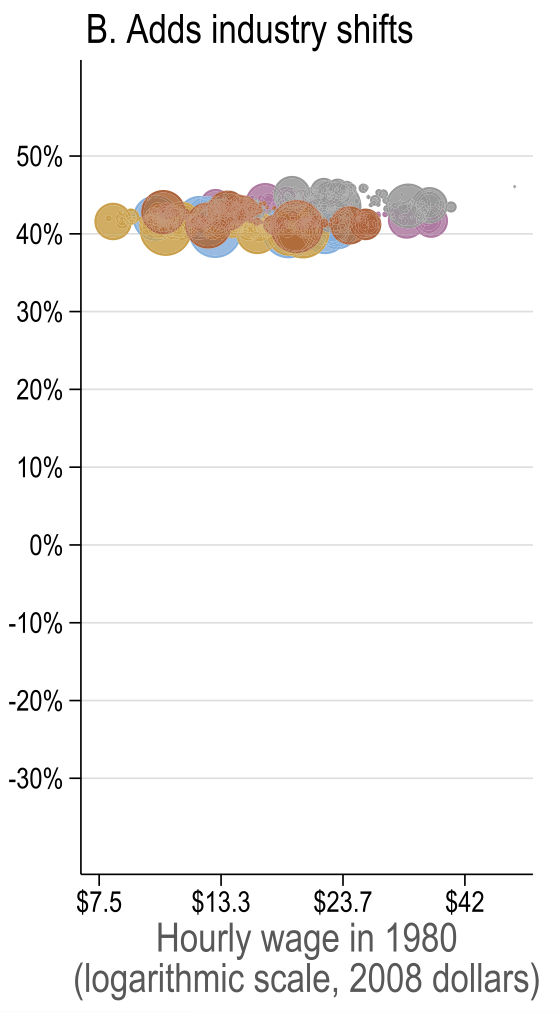
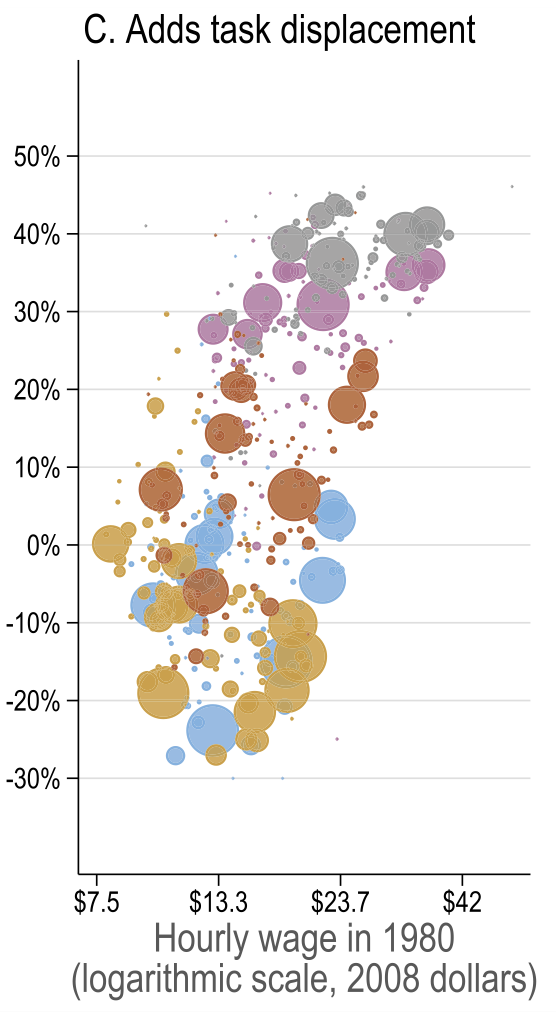
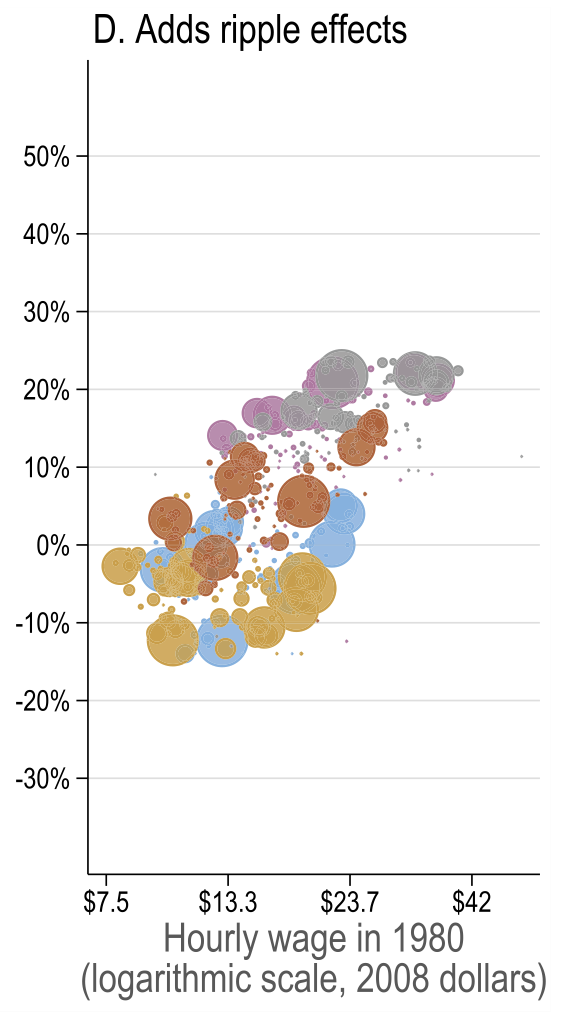
Source: Figure 7
Acemoglu and Restrepo (2022)
Model fit
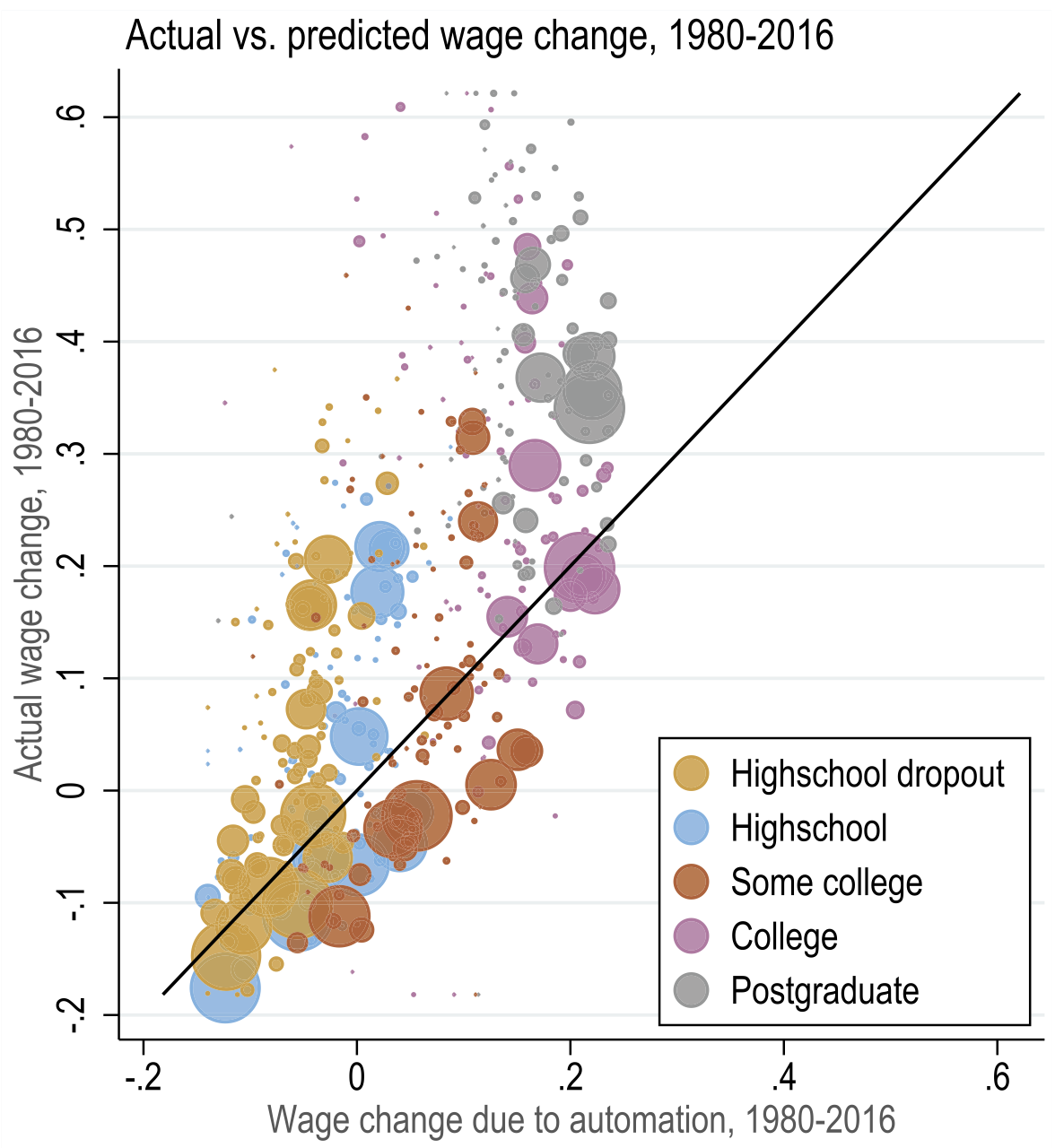
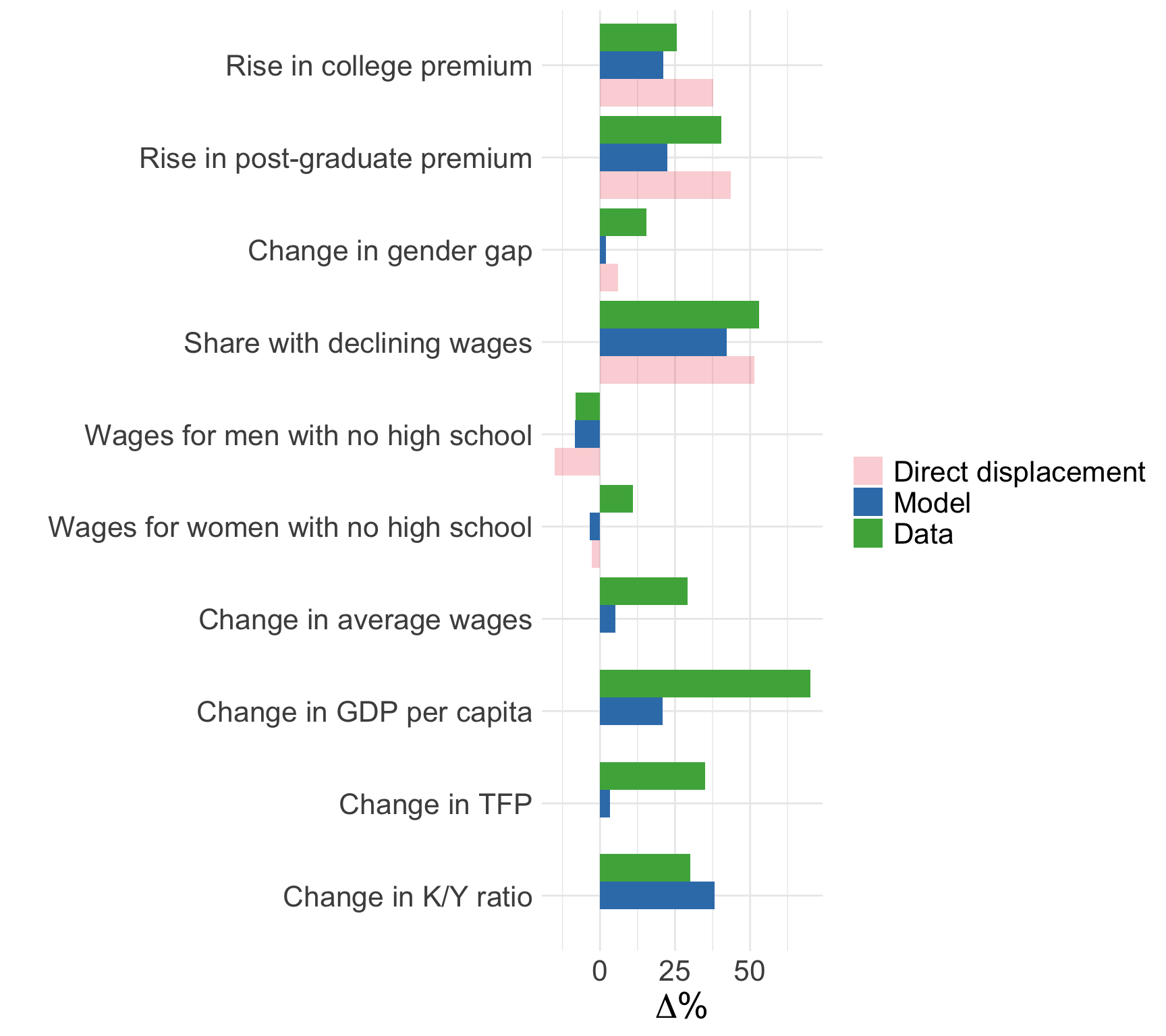
Summary
Two theories linking technological advancements and labour markets
Canonical model (SBTC)
- Simple application of two-factor labour demand theory
- Empirically attractive characterization of between-group inequality
- Fails to account for within-group inequality, polarization, and displacement
Task-based model (automation)
- Rich model linking skills to tasks to output
- Explains large share of changes in the wage structure since 1980s
Next: Labour market discrimination
Appendix: derivation of wage equations
The firm problem is to choose entire schedules \(\left(l(i), m(i), h(i)\right)_{i=0}^1\) to
\[ \max PY - w_L L - w_M M - w_H H \]
Consider FOC wrt \(l(j)\):
\[ PY \int_0^1 \frac{1}{y(j)} A_L \alpha_L(j) \text{d}i - w_L \int_0^1 \text{d}i = 0 \]
We normalised \(P = 1\); therefore, the FOC can be rewritten as
\[ \frac{Y}{y(j)} A_L \alpha_L(j) = w_L \]
On the next slide, we see that \(\frac{Y}{y(j)} = \frac{1}{p(j)}\).
Similar argument for \(w_M\) and \(w_H\).
Appendix: derivation of skill allocations
Numeraire price (\(P=1\)) is chosen such that \(\frac{y(i)}{Y} = \frac{p(i)}{P} = p(i), \forall i \in [0, 1]\)
Therefore, productivity of \(L\) is \(\frac{Y}{L} = \frac{y(i)}{p(i)L} = \frac{y(j)}{p(j)L}, \forall i \neq j < I_L\)
If we plug in definition of \(y(i)\) and notice that only \(l(i)\) matters when \(i < I_L\), then
\[ \frac{A_L \alpha_L(i) l(i)}{p(i) L} = \frac{A_L \alpha_L(j)l(j)}{p(j)L} \]
Given the wage equations in Law of one wage, we know \(\frac{A_L\alpha_L(i)}{p(i)} = \frac{A_L \alpha_L(j)}{p(j)}\). Therefore, \(l(i) = l(j), \quad \forall i\neq j < I_L\).
Plug it into the market clearing condition for \(L\)
\[ L = \int_0^{I_L} l(i) \text{d}i = l I_L \quad \Longrightarrow \quad l(i) = l = \frac{L}{I_L}, \forall i < I_L \]
Similar argument for \(m(i)\) and \(h(i)\).