8. Technological shift and labour markets
KAT.TAL.322 Advanced Course in Labour Economics
Nurfatima Jandarova
September 17, 2025
Technological shift and the labour market
Stylised facts
Labour market of educated workers
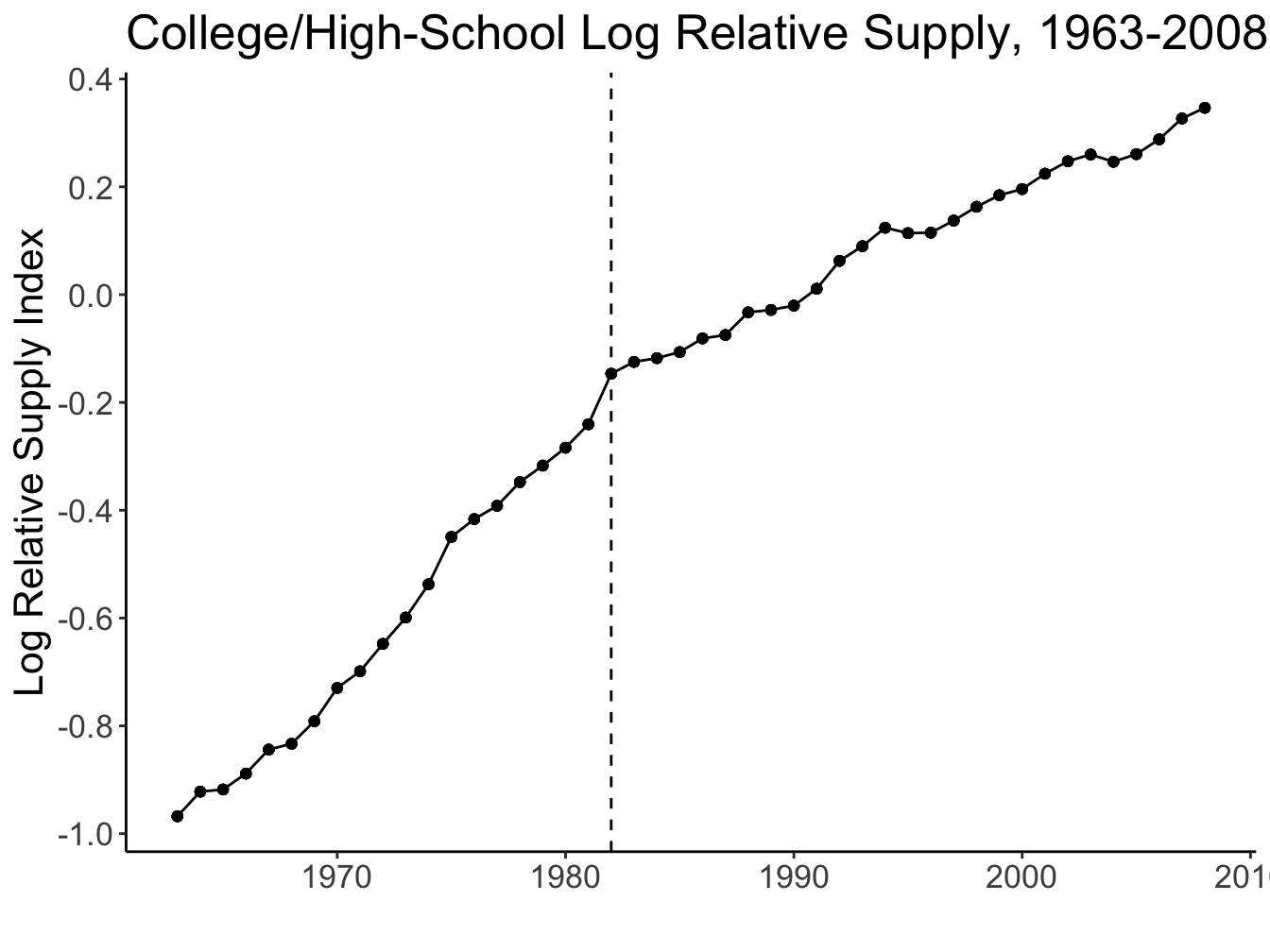
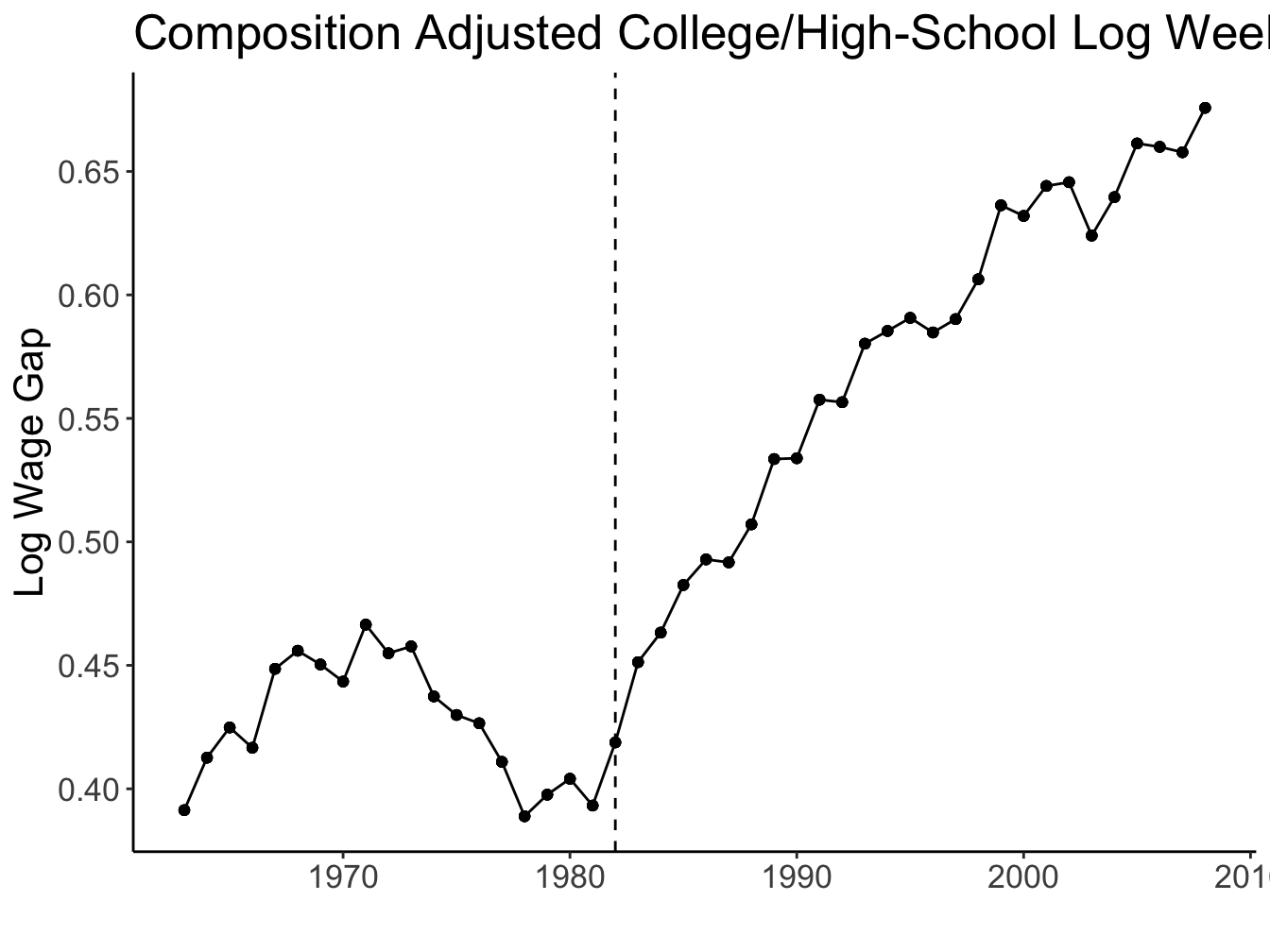
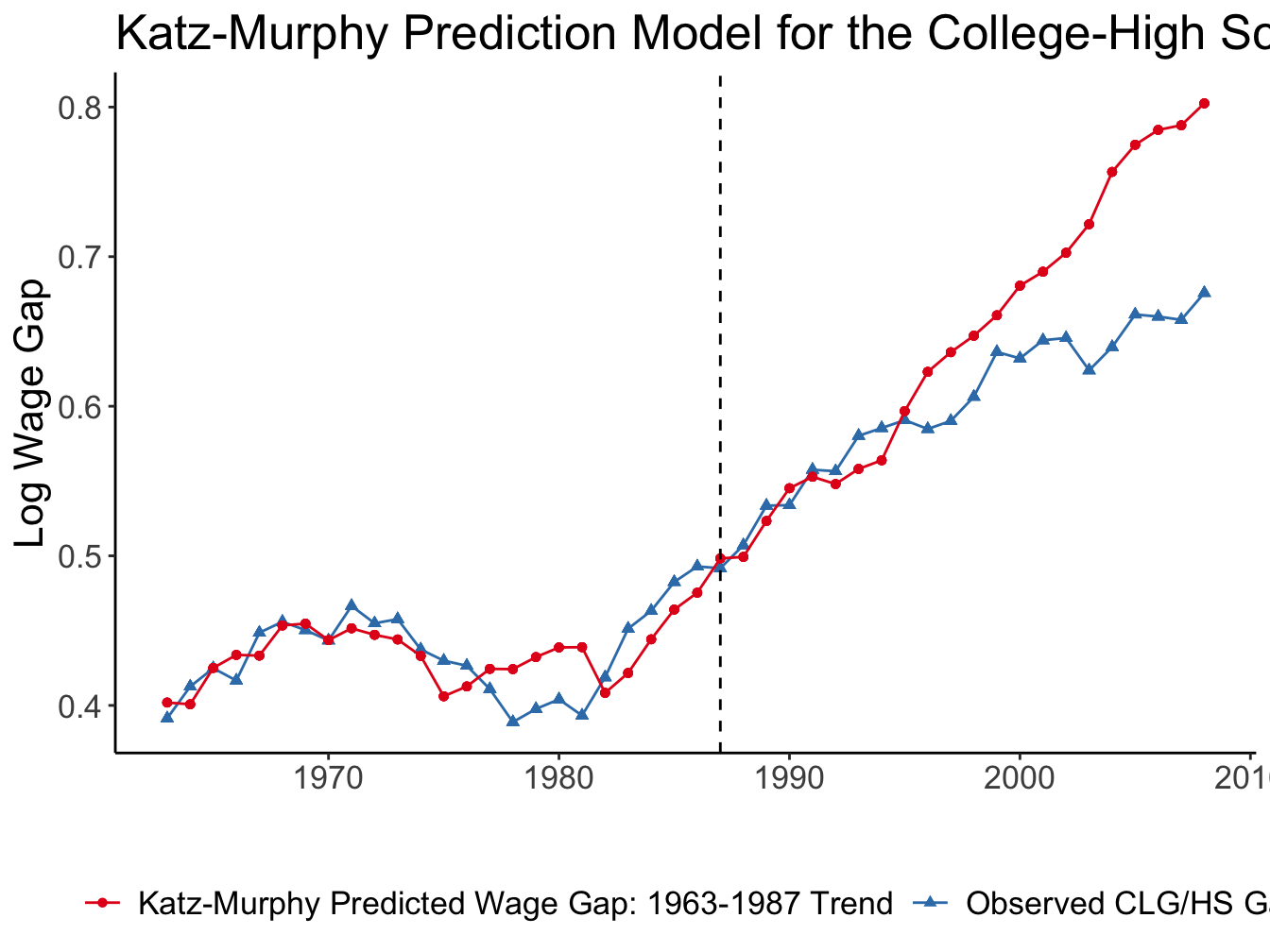
Source: Figures 1 and 2 (Acemoglu and Autor 2011)
Canonical model
Canonical model
Overview
Two types of labour: high- and low-skill
Typically, high edu and low edu (can be relaxed)Skill-biased technological change (SBTC)
New technology disproportionately ↑ high-skill labour productivityHigh- and low-skill are imperfectly substitutable
Typically, CES production function with elasticity of substitution σCompetitive labour market
Canonical model
Production function
Y=[(ALL)σ−1σ+(AHH)σ−1σ]σσ−1
AL and AH are factor-augmenting technology terms
σ∈[0,∞) is the elasticity of substitution
- σ>1 gross substitutes
- σ<1 gross complements
- σ=0 perfect complements (Leontieff production)
- σ→∞ perfect substitutes
- σ=1 Cobb-Douglas production
Canonical model
Rationalisation of CES production function
- Single output Y; H and L are imperfect substitutes
- Two goods YH=AHH and YL=ALL; CES utility of consumers [Yσ−1σL+Yσ−1σH]σσ−1
- Combination of the 1. and 2.
Supply of H and L assumed inelastic ⇒ study only firm side
Canonical model
Equilibrium wages
wL=Aσ−1σL[Aσ−1σL+Aσ−1σH(HL)σ−1σ]1σ−1wH=Aσ−1σH[Aσ−1σL(HL)−σ−1σ+Aσ−1σH]1σ−1
Comparative statics:
- ∂wL∂H/L>0 low-skill wage rises with HL
- ∂wH∂H/L<0 high-skill wage falls with HL
- ∂wi∂AL>0 and ∂wi∂AH>0, ∀i∈{L,H}
Canonical model
Skill premium
wHwL=(AHAL)σ−1σ(HL)−1σ
Δ relative supply
∂lnwHwL∂lnHL=−1σ<0
Δ technology
∂lnwHwL∂lnAHAL=σ−1σ≶0
- Gross substitutes: σ>1⇒∂lnwH/wL∂lnAH/AL>0
- Gross complements: σ<1⇒∂lnwH/wL∂lnAH/AL<0
- Cobb-Douglas: σ=1⇒∂lnwH/wL∂lnAH/AL=0
Tinbergen’s race in the data
Katz and Murphy (1992)
The log-equation of skill premium is extremely attractive for empirical analysis
lnwH,twL,t=σ−1σln(AH,tAL,t)−1σln(HtLt)
Assume a log-linear trend in relative productivities
ln(AH,tAL,t)=α0+α1t
and plug it into the log skill premium equation:
lnwH,twL,t=σ−1σα0+σ−1σα1t−1σln(HtLt)
Tinbergen’s race in the data
Katz and Murphy (1992)
Estimated the skill premium equation using the US data in 1963-87 lnωt=cons+0.027(0.005)×t−0.612(0.128)×ln(HtLt)
Implies elasticity of substitution σ≈10.612= 1.63
Agrees with other estimates that place σ between 1.4 and 2 (Acemoglu and Autor 2011)
Tinbergen’s race in the data
Very close fit up to mid-1990s, diverge later
Fit up to 2008 implies σ≈ 2.95
Accounting for divergence:
non-linear time trend in lnAHAL
brings σ back to 1.8, but implies AHAL slowed downdifferentiate labour by age/experience as well
Canonical model
Summary
- Simple link between wage structure and technological change
- Attractive explanation for college/no college wage inequality1
- Average wages ↑ (follows from ∂wi/∂AH and ∂wi/∂AL)
However, the model cannot explain other trends observed in the data:
- Falling wL
- Earnings polarization
- Job polarization
Also silent about endogeneous adoption or labour-replacing technology.
Unexplained trend: falling real wages
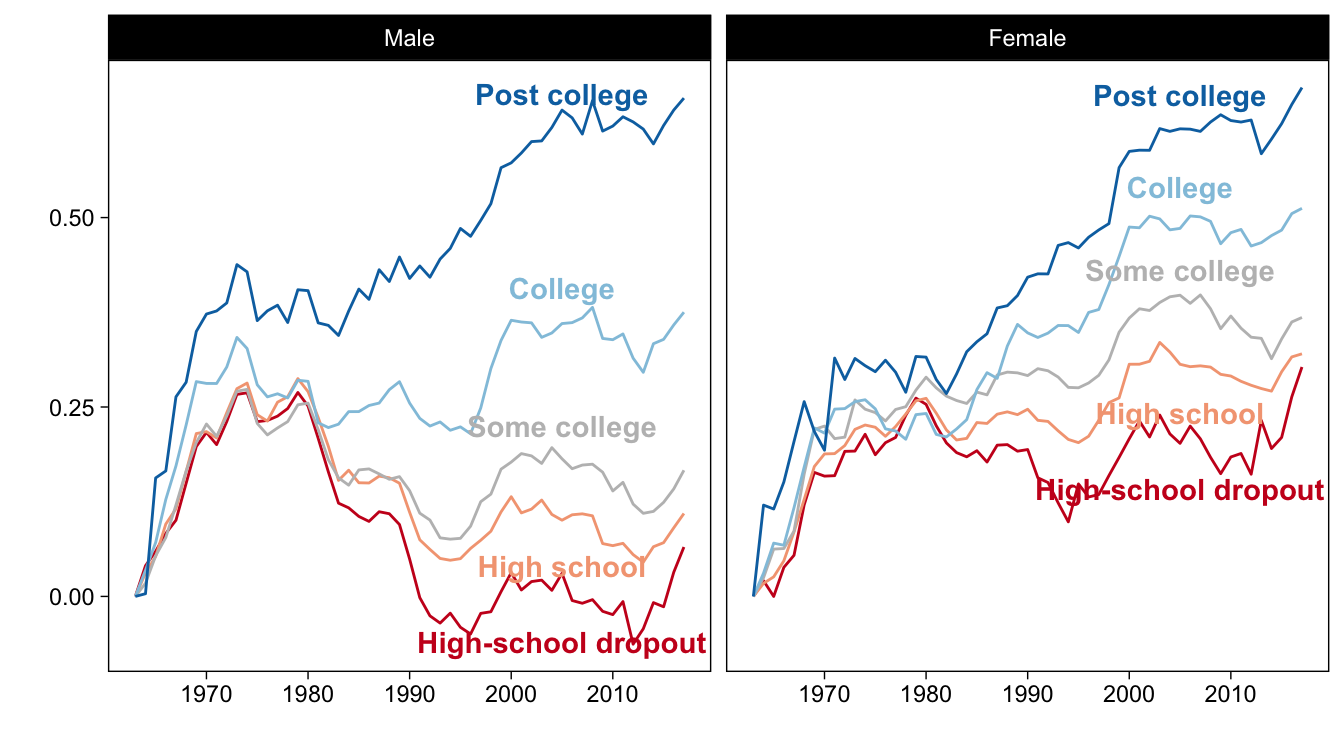
Source: Figure 1 (Autor 2019)
Unexplained trend: earnings polarization
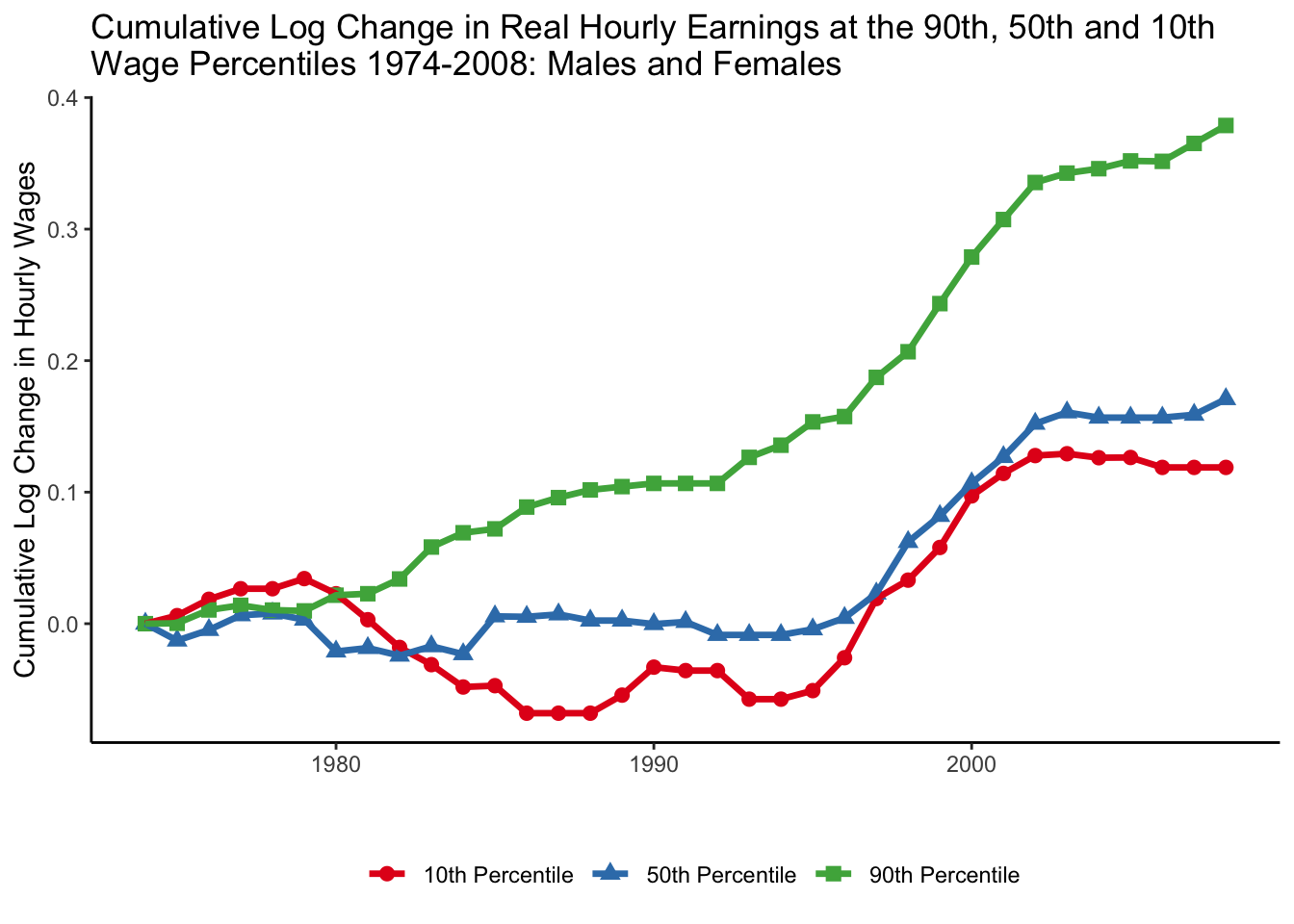
Source: Figure 8 (Acemoglu and Autor 2011)
Unexplained trend: job polarization
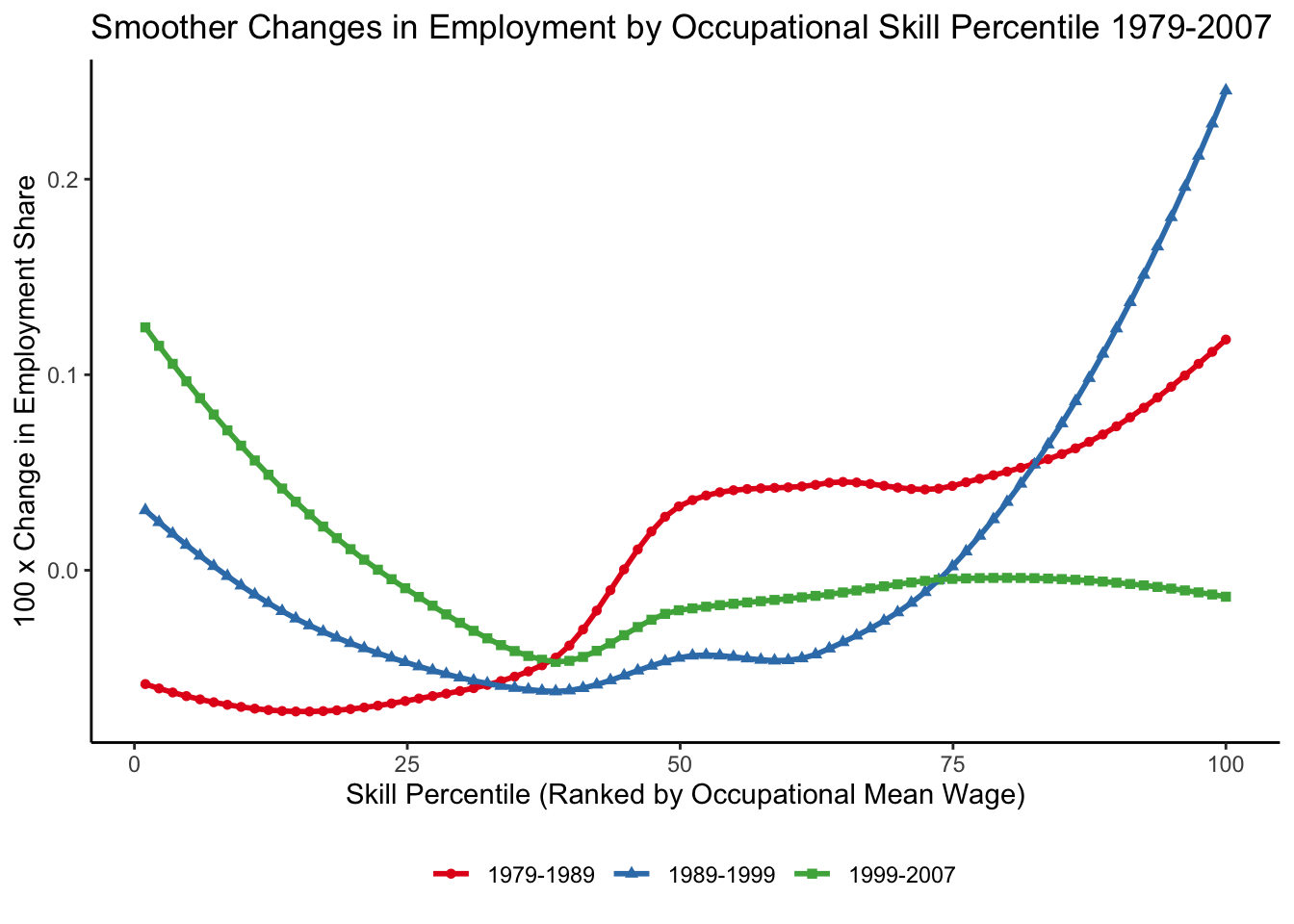
Source: Figure 10 (Acemoglu and Autor 2011)
Task-based model
Task-based model
Overview
Task is a unit of work activity that produces output
Skill is a worker’s endowment of capabilities for performing tasks
Key features:
- Tasks can be performed by various inputs (skills, machines)
- Comparative advantage over tasks among workers
- Multiple skill groups
- Consistent with canonical model predictions
Task-based model
Production function
Unique final good Y produced by continuum of tasks i∈[0,1]
Y=exp[∫10lny(i)di]
Three types of labour: H, M and L supplied inelastically.
y(i)=ALαL(i)l(i)+AMαM(i)m(i)+AHαH(i)h(i)+AKαK(i)k(i)
AL,AM,AH,AK are factor-augmenting technologies
αL(i),αM(i),αH(i),αK(i) are task productivity schedules
l(i),m(i),h(i),k(i) are production inputs allocated to task i
Task-based model
Comparative advantage assumption
αL(i)/αM(i) and αM(i)/αH(i) are continuously differentiable and strictly decreasing.
Market clearing conditions
∫10l(i)di≤L∫10m(i)di≤M∫10h(i)di≤H
Task-based model
Equilibrium without machines
Lemma 1
Given comparative advantage assumption, there exist IL and IH such that
Note that boundaries IL and IH are endogenous
This gives rise to the substitution of skills across tasks
Task-based model
Law of one wage
Output price is normalised to 1 ⇒exp[∫10lnp(i)di]=1
All tasks employing a given skill pay corresponding wage
wL=p(i)ALαL(i),∀i∈[0,IL]wM=p(i)AMαM(i),∀i∈(IL,IH]wH=p(i)AHαH(i),∀i∈(IH,1]
Task-based model
Skill allocations
Given the law of one wage, we can show that
l(i)=l(i′)⇒l(i)=LIL∀i∈[0,IL]m(i)=m(i′)⇒m(i)=MIH−IL∀i∈(IL,IH]h(i)=h(i′)⇒h(i)=H1−IH∀i∈(IH,1]
Task-based model
Endogenous thresholds: no arbitrage
Threshold task IH: equally profitable to produce with either H or M skills
AMαM(IH)MIH−IL=AHαH(IH)H1−IH
Similarly, for IL:
ALαL(IL)LIL=AMαM(IL)MIH−IL
Task-based model
Endogenous thresholds: no arbitrage
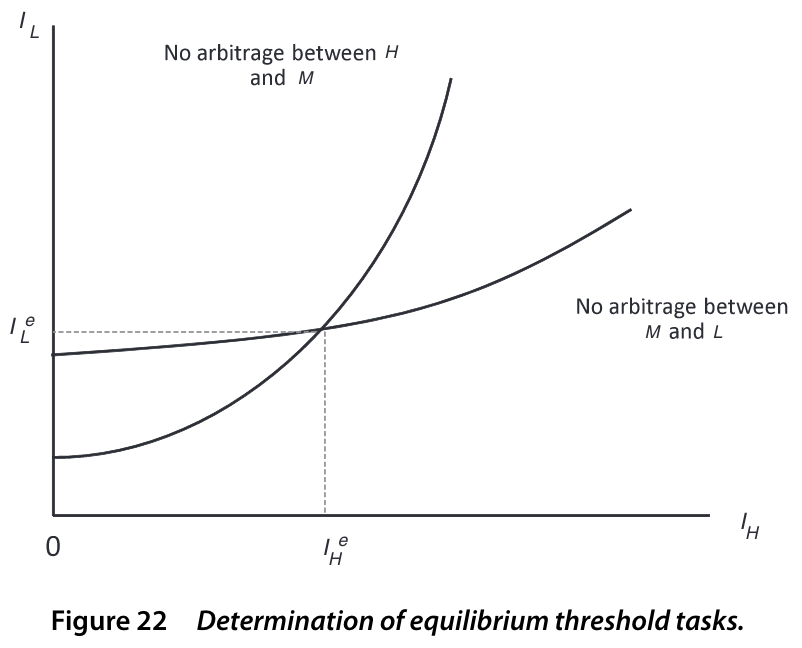
Task-based model
Comparative statics: wage elasticities
dlnwH/wLdlnAH>0dlnwM/wLdlnAH<0dlnwH/wMdlnAH>0dlnwH/wLdlnAM⪋0dlnwM/wLdlnAM>0dlnwH/wMdlnAM<0dlnwH/wLdlnAL<0dlnwM/wLdlnAL<0dlnwH/wMdlnAL>0
Task-based model
Comparative statics: ↑AH
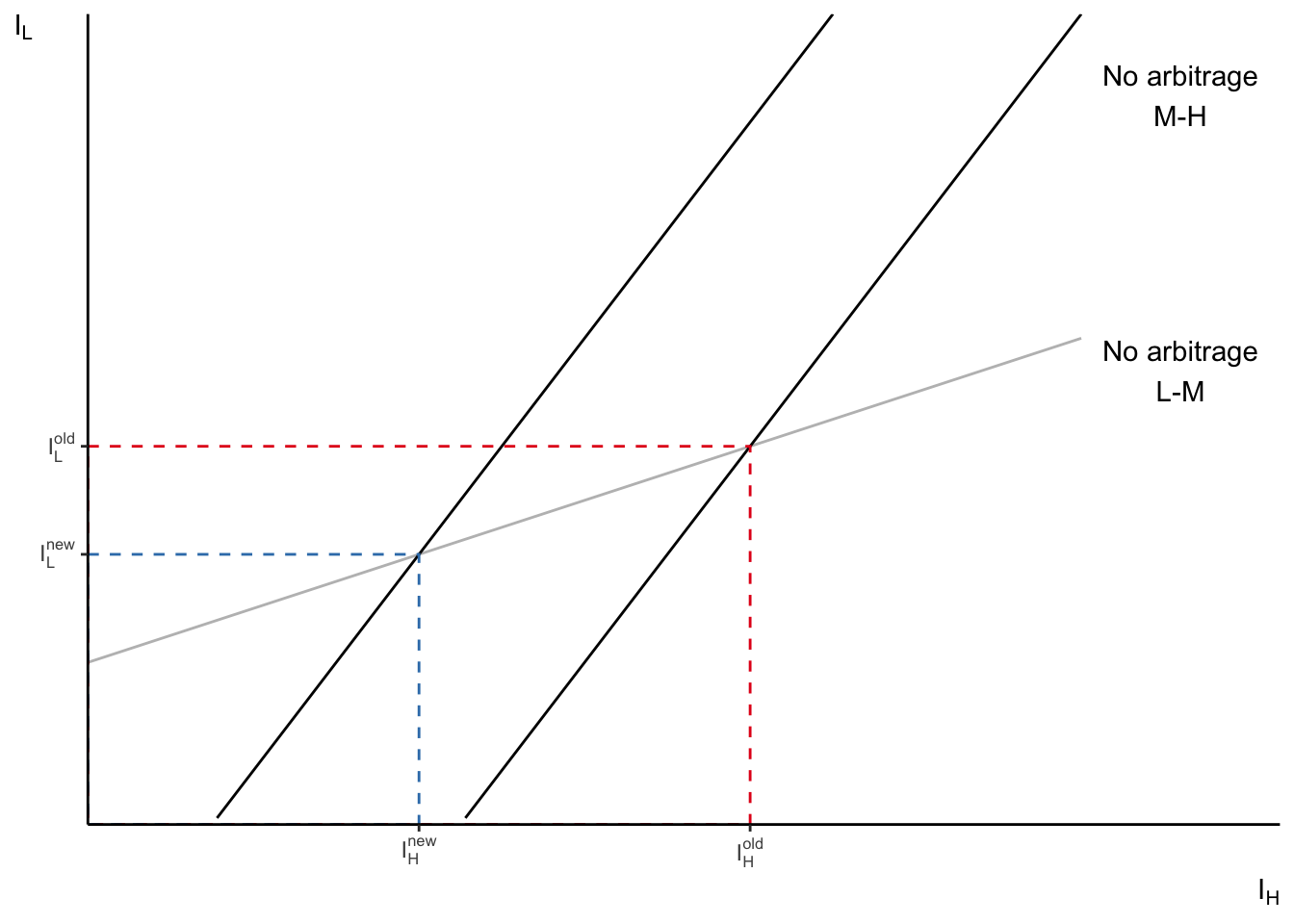
Source: Figure 25 (Acemoglu and Autor 2011)
Task-based model
Task replacing technologies
Start from initial equilibrium without machines
Assume in [I_,ˉI]⊂[IL,IH] machines outperform M. Otherwise, αK(i)=0.
How does it change the equilibrium?
Task-based model
Task replacing technologies
Assume comparative advantage of H over M stronger than M over L
- wH/wM increases
- wM/wL decreases
- wH/wL↑(↓) if |β′L(IL)IL|<>|β′H(IH)(1−IH)|
Task-based model
Endogenous supply of skills
Each worker j is endowed with some amount of each skill lj,mj,hj
Workers allocate time to each skill given
tjl+tjm+tjh≤1wLtjllj+wMtjmmj+wHtjhhj
Comparative advantage: hjmj and mjlj are decreasing in j
Then, there exist J⋆(wHwM) and J⋆⋆(wMwL)
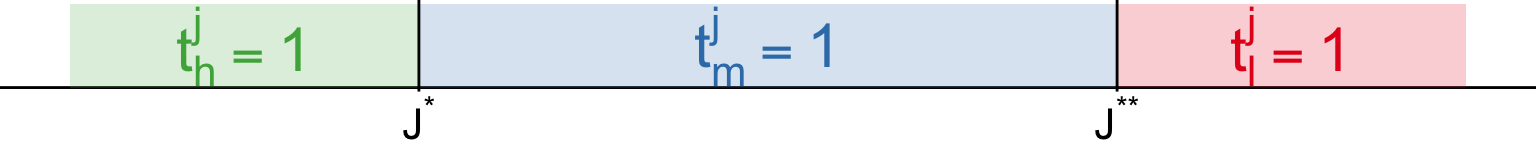
Task-based model
Illustration in the data
Suppose ↑AH⇒↑wHwM,↓wMwL.
Use occupational specialization at some t=0 as comparative advantage.
- γisejk share of 1959 population employed in i occupations, ∀i∈{H,M,L}
Δwsejkτ=∑t[βHtγHsejk+βLtγLsejk]1{τ=t}+δτ+ϕe+λj+πk+esejkτ
Descriptive regression informed by the model!
Task-based model
Illustration in the data
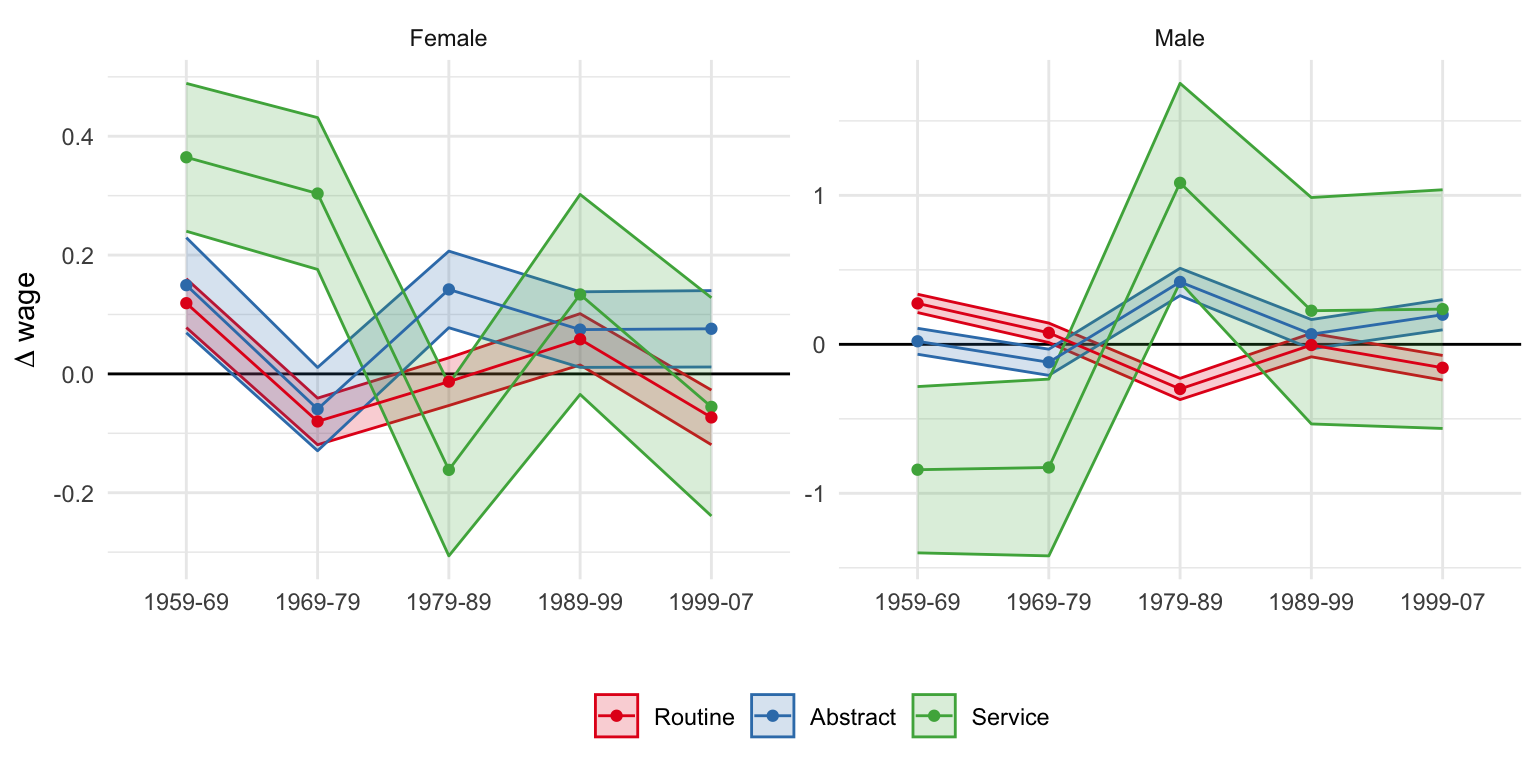
Source: Table 10 (Acemoglu and Autor 2011)
Task-based model
Summary
- A rich model that can accommodate numerous scenarios
- Outsourcing tasks to lower-cost countries
- Endogenous technological change
- Creation of new tasks
- Useful tool to study effect on inequality and job polarization
Empirical results
Acemoglu and Restrepo (2022)
Environment
Multi-sector model with imperfect substitution between inputs
Task displacementdirectg=∑i∈IωigωRgiωRi(−dlnsL,autoi)
ωig - share of wages earned by worker group g in industry i
(exposure to industry i)at t=0ωRgiωRi - specialization of group g in routine tasks R within industry i at t=0
−dlnsL,autoi - % decline in industry i’s labour share due to automation
attribute 100% of the decline to automation
predict given industry adoption of automation technology
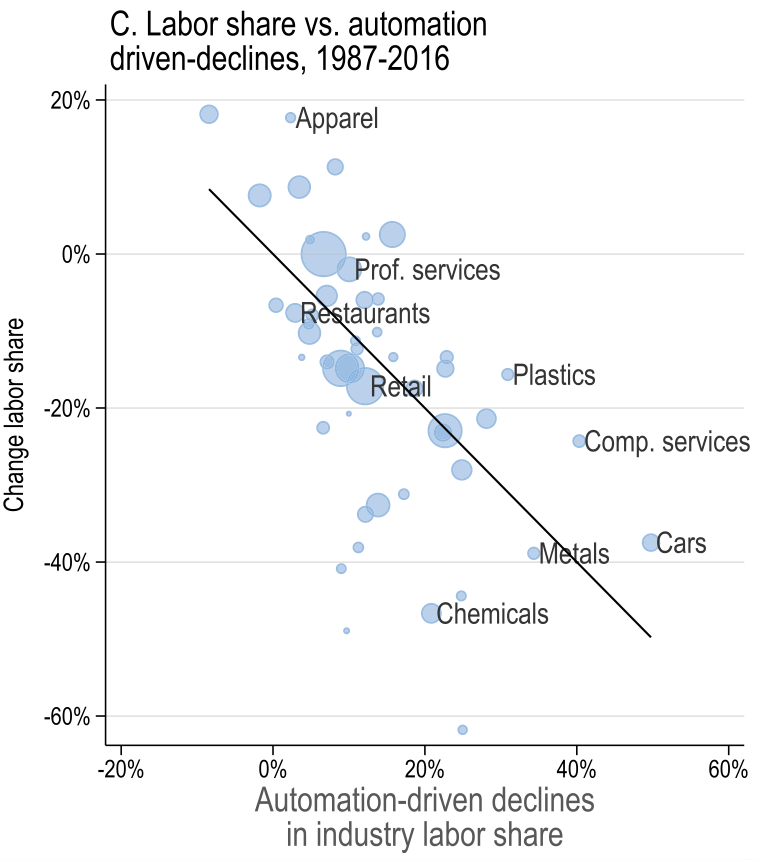
Acemoglu and Restrepo (2022)
Task displacement
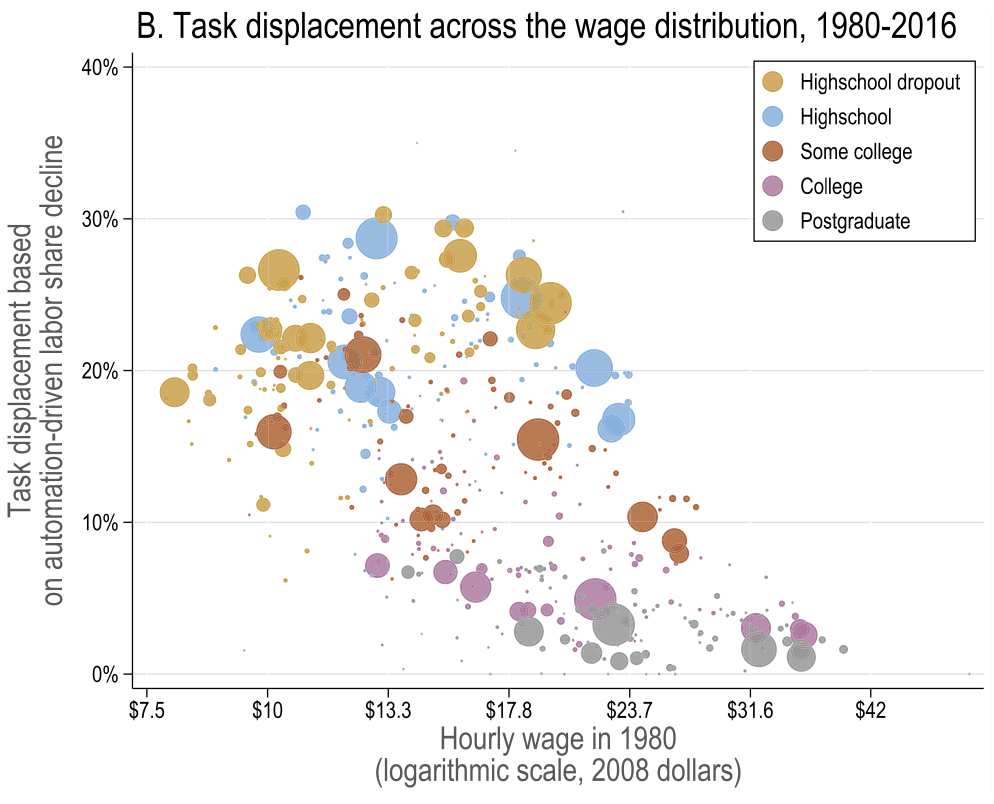
Source: Figure 5
Acemoglu and Restrepo (2022)
Task displacement and changes in real wages
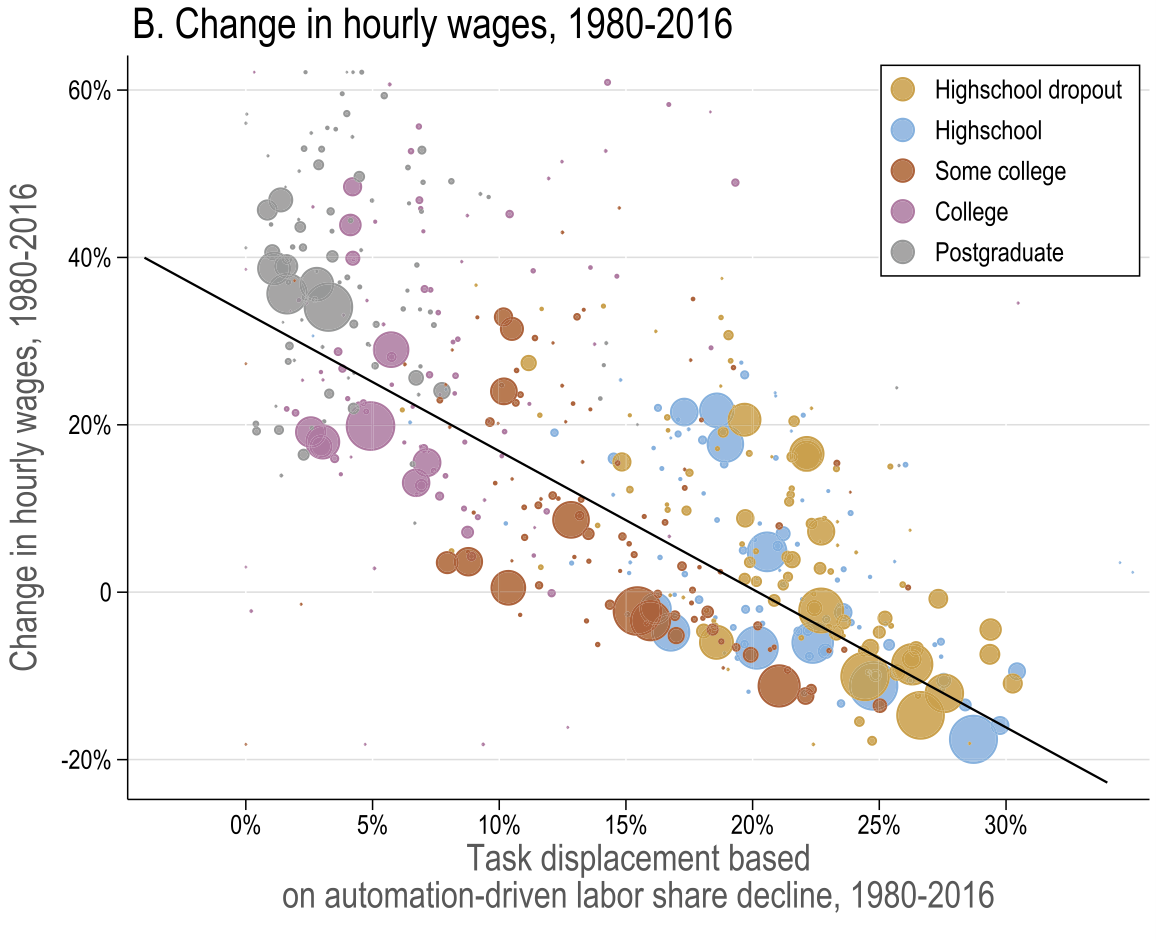
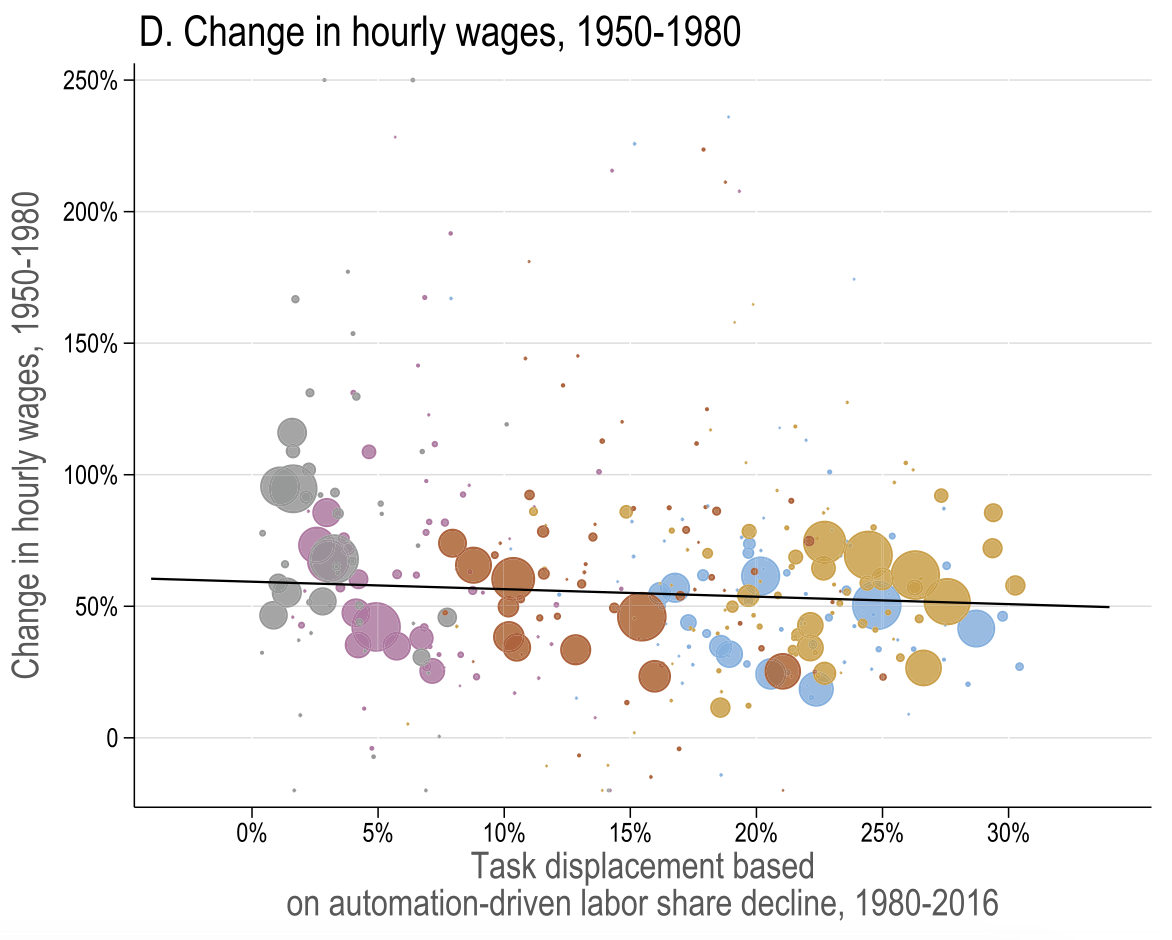
Acemoglu and Restrepo (2022)
General equilibrium results
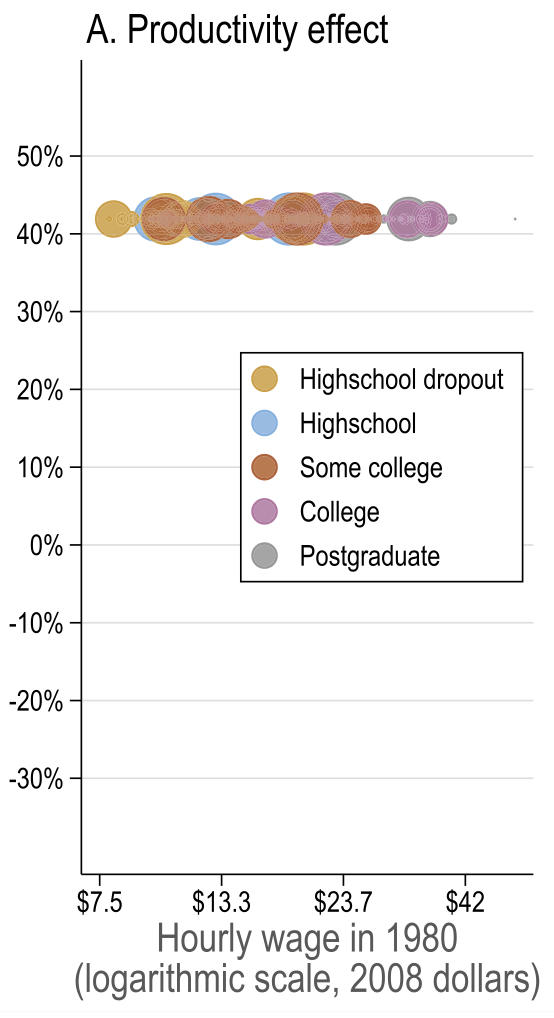
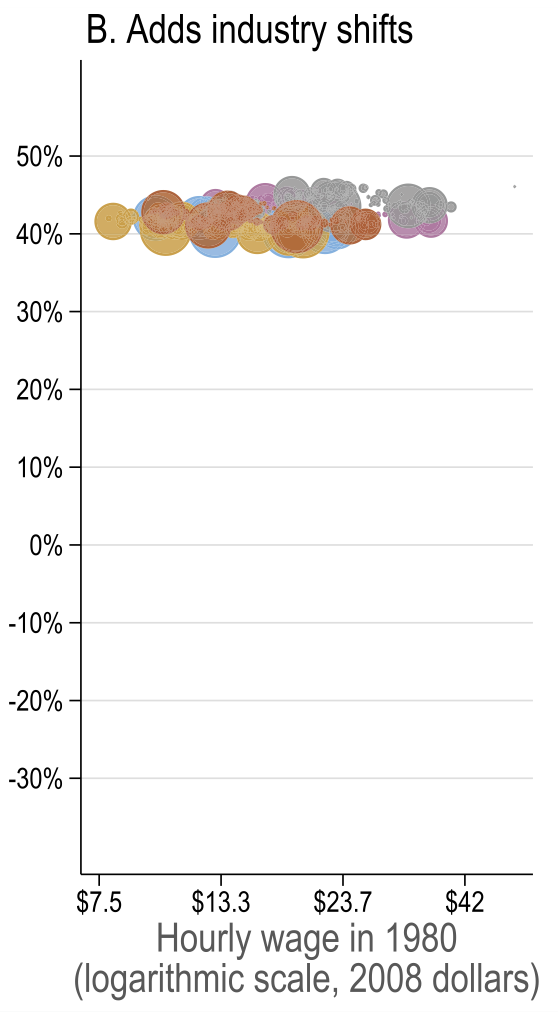
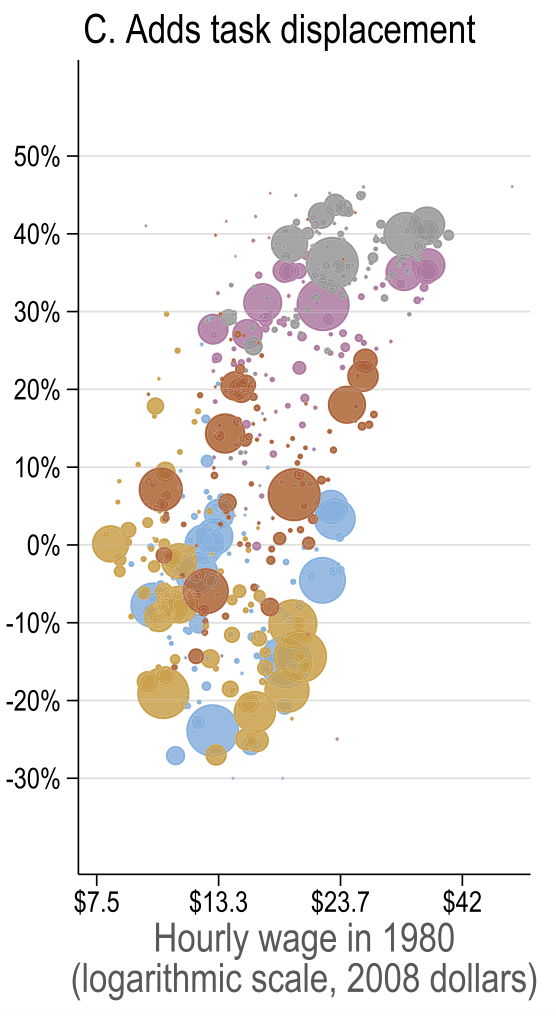
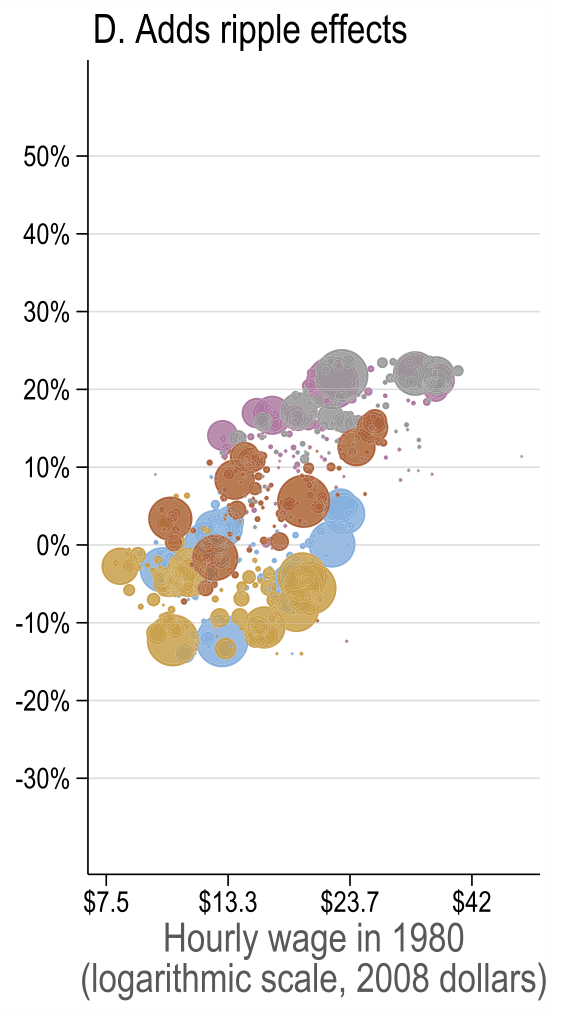
Source: Figure 7 (Acemoglu and Restrepo 2022)
Acemoglu and Restrepo (2022)
Model fit
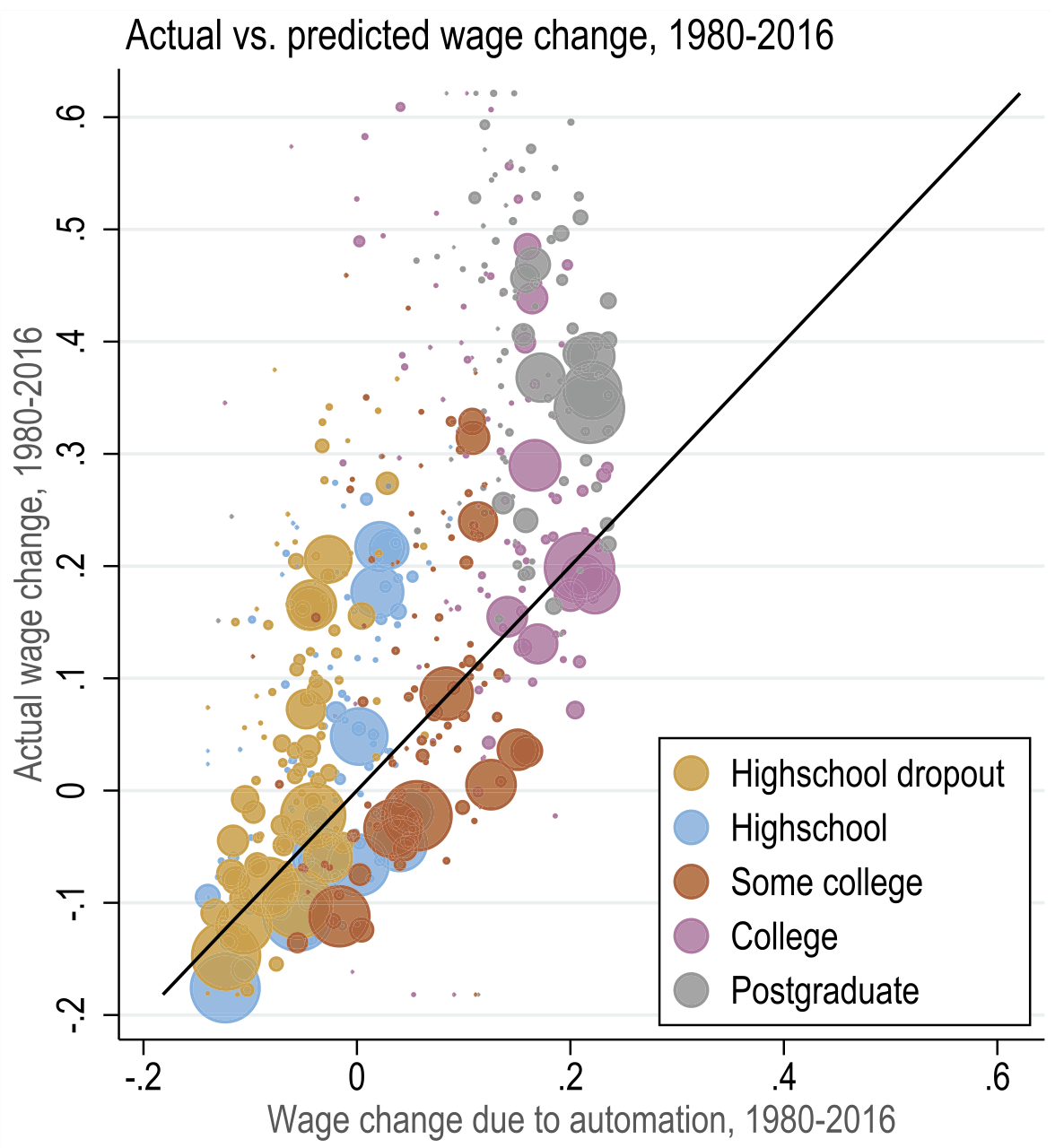
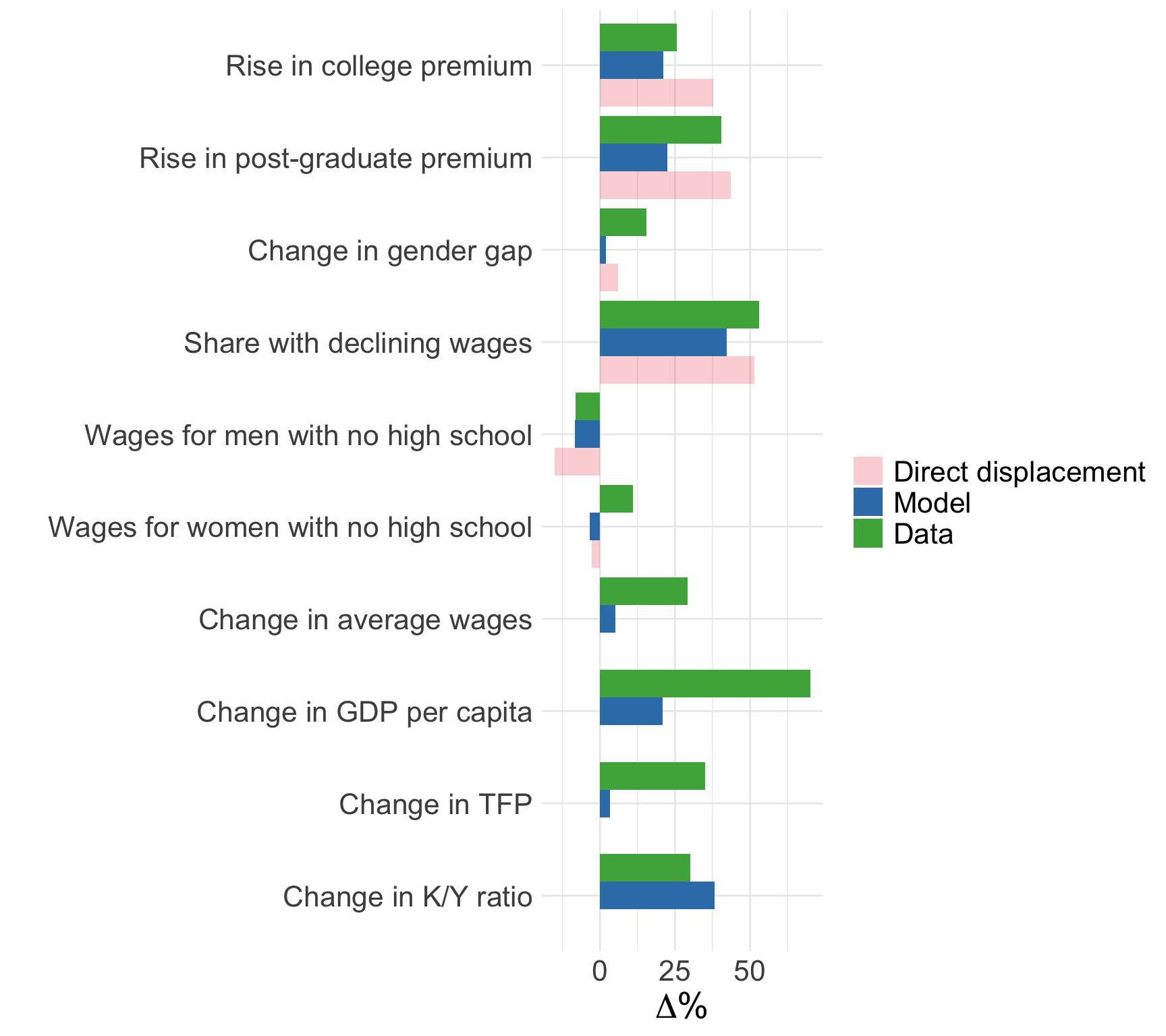
Summary
Two theories linking technological advancements and labour markets
Canonical model (SBTC)
- Simple application of two-factor labour demand theory
- Empirically attractive characterization of between-group inequality
- Fails to account for within-group inequality, polarization, and displacement
Task-based model (automation)
- Rich model linking skills to tasks to output
- Explains large share of changes in the wage structure since 1980s
Next lecture: Labour market discrimination on 22 Sep
Appendix: derivation of wage equations
The firm problem is to choose entire schedules (l(i),m(i),h(i))1i=0 to
max(l(i),m(i),h(i))1i=0PY−wLL−wMM−wHH
We normalised P=1. Consider FOC wrt l(i):
Yy(i)ALαL(i)=wL,∀i∈[0,IL]
In equilibrium, all L-type workers must be paid same amount ⇒
p(i)ALαL(i)=wL,∀i∈[0,IL]
Similar argument for wM and wH.
Appendix: derivation of skill allocations
Given the law of one price (wage) we can also write that
p(i)αL(i)l(i)=p(i′)αL(i′)l(i′),∀i,i′∈[0,IL]
Given the Appendix: derivation of wage equations, it implies that
l(i)=l(i′)=l,∀i,i′∈[0,IL]
Plug it into the market clearing condition for L
L=∫IL0l(i)di=l⋅IL⟹l(i)=l=LIL,∀i∈[0,IL]
Similar argument for m(i)=MIH−IL and h(i)=H1−IH.
References
Acemoglu, Daron, and David Autor. 2011. “Chapter 12 - Skills, Tasks and Technologies: Implications for Employment and Earnings.” In Handbook of Labor Economics, edited by David Card and Orley Ashenfelter, 4:1043–1171. Elsevier. https://doi.org/10.1016/S0169-7218(11)02410-5.
Acemoglu, Daron, and Pascual Restrepo. 2018. “The Race Between Man and Machine: Implications of Technology for Growth, Factor Shares, and Employment.” American Economic Review 108 (6): 1488–1542. https://doi.org/10.1257/aer.20160696.
———. 2022. “Tasks, Automation, and the Rise in U.S. Wage Inequality.” Econometrica 90 (5): 1973–2016. https://doi.org/10.3982/ECTA19815.
Autor, David H. 2019. “Work of the Past, Work of the Future.” AEA Papers and Proceedings 109 (May): 1–32. https://doi.org/10.1257/pandp.20191110.
Autor, David H., Frank Levy, and Richard J. Murnane. 2003. “The Skill Content of Recent Technological Change: An Empirical Exploration*.” The Quarterly Journal of Economics 118 (4): 1279–1333. https://doi.org/10.1162/003355303322552801.
Katz, Lawrence F., and Kevin M. Murphy. 1992. “Changes in Relative Wages, 1963-1987: Supply and Demand Factors.” The Quarterly Journal of Economics 107 (1): 35–78. https://doi.org/10.2307/2118323.
8. Technological shift and labour markets KAT.TAL.322 Advanced Course in Labour Economics Nurfatima Jandarova September 17, 2025