2. Labour Supply
KAT.TAL.322 Advanced Course in Labour Economics
August 27, 2025
Labour supply
How people choose
- whether to work, and
- how much to work
Static model
Static labour supply
Model
- Utility from consumption of goods (C) and leisure (L): U(C,L).
- Total time endowment L0
- Agent chooses h how much time to work such that L=L0−h.
- Budget constraint is C≤wh+Y⇒C+wL≤wL0+Y
- w is real hourly wage
- Y is non-labour income
maxC,hU(C,L0−h)subject toC≤wh+Y
Static labour supply
Allocation of time in the data
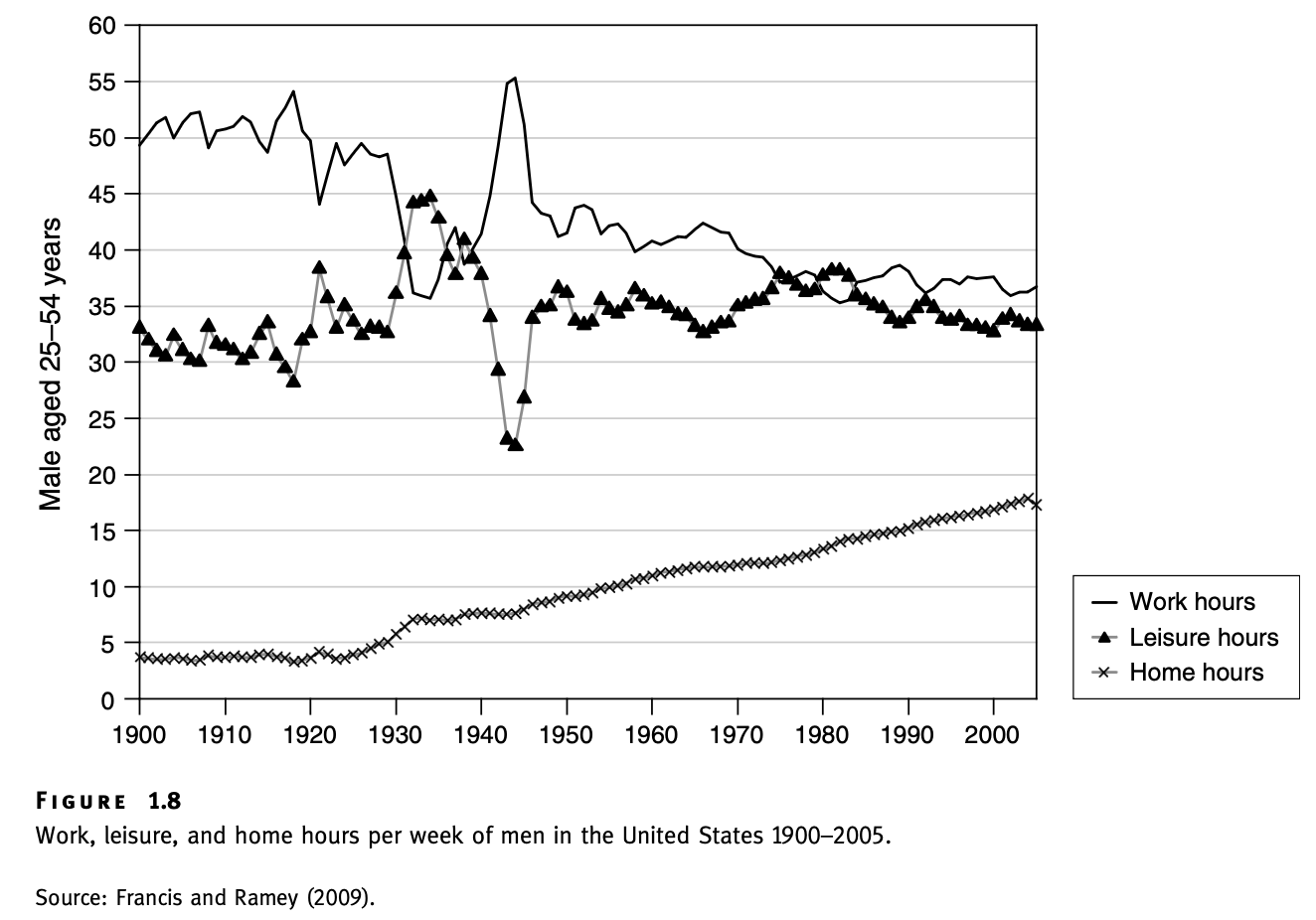
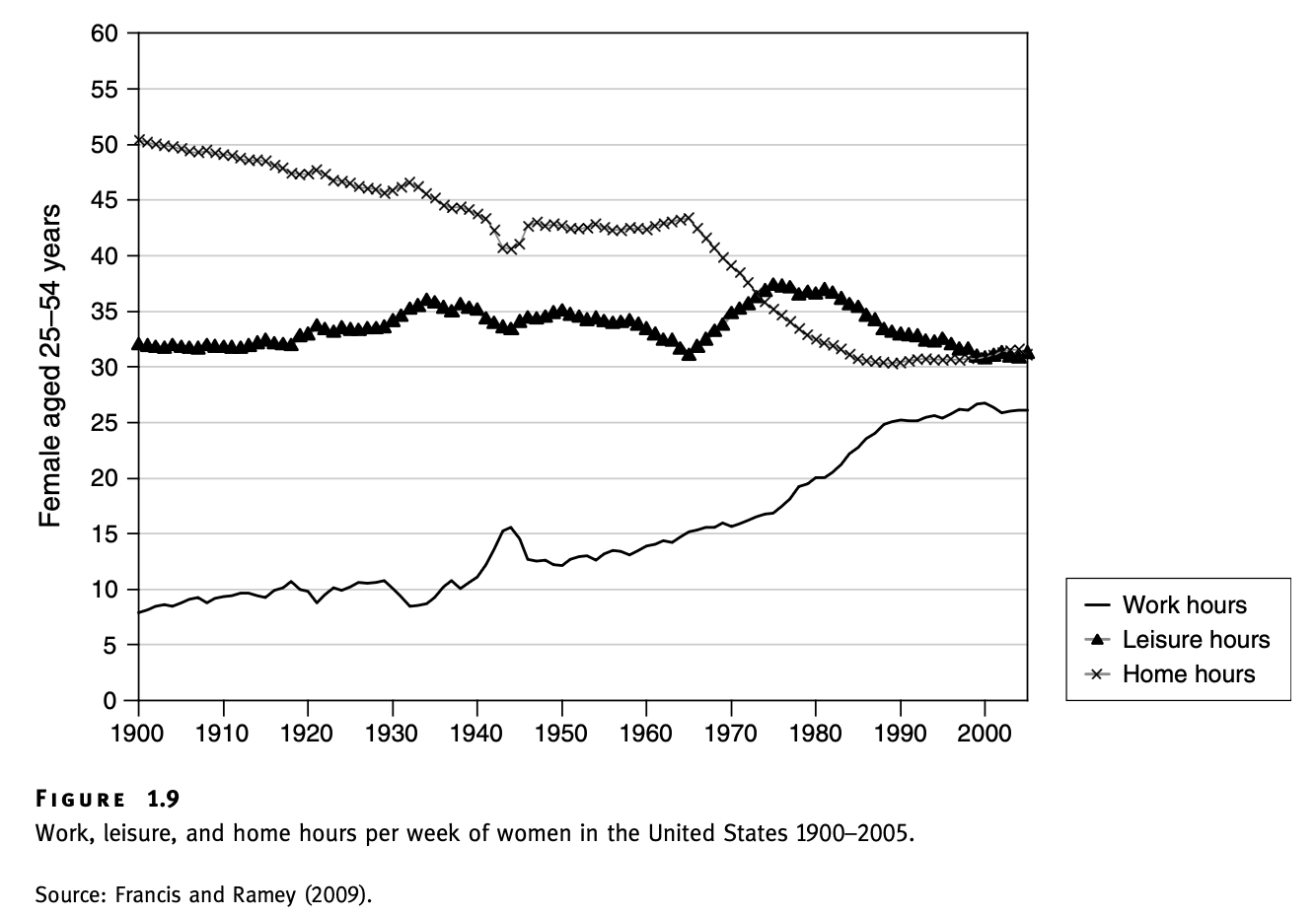
Static labour supply
Solution
First-order conditions of the Lagrangian are
UC(C,L)=λUL(C,L)=λw
Solution pair C∗(w,Y) and h∗(w,Y) satisfies
UL(C∗,L∗)UC(C∗,L∗)=wandC∗=wh∗+Y
Static labour supply
Solution
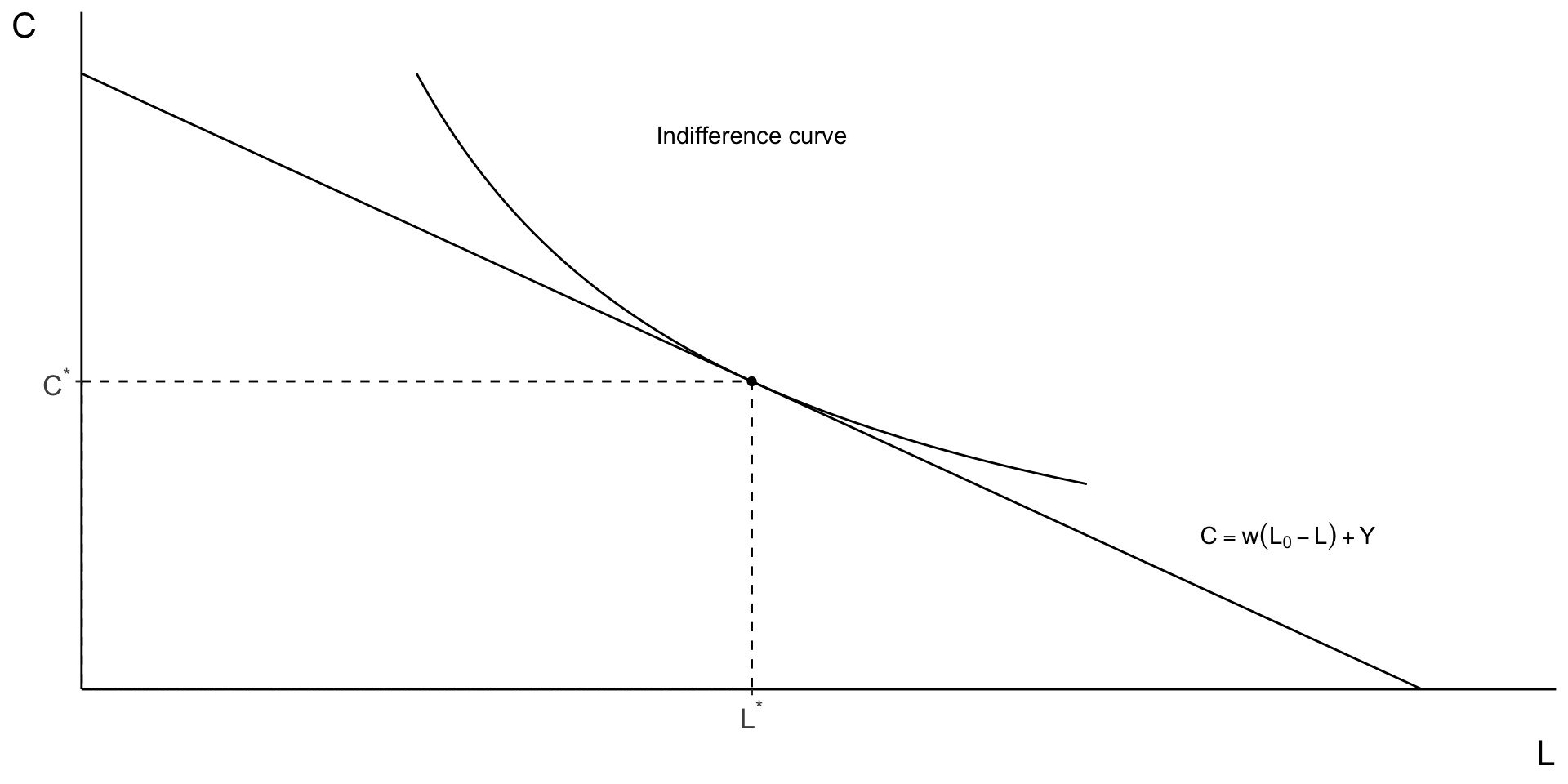
Static labour supply
Comparative statics
How does optimal labour supply change with w?
Marshallian (uncompensated) wage elasticity: εhw=∂lnh∗∂lnw
Hicksian (compensated) wage elasticity: ηhw=∂lnˆh∂lnw
Decomposition into substitution and income effects:
εhw=ηhw+whYεhY
Static labour supply
Comparative statics

Source: Wikipedia
Static labour supply
Labour supply curve

Source: Wikipedia
Household model
Intrahousehold labour supply
Unitary model
Household represented by single utility function U(C,L1,L2)
Budget constraint C+w1L1+w2L2≤Y1+Y2+(w1+w2)L0
Simple extension of static model
Consumption depends on total resources only
Not consistent with empirical studies
Intrahousehold labour supply
Collective model
Individual utility functions U1(C1,L1),U2(C2,L2)
Budget constraint C1+C2+w1L1+w2L2≤R1+R2+(w1+w2)L0
maxC1,C2,L1,L2U1(C1,L1)s.t.budget constraintU2(C2,L2)≥ˉU2
Intrahousehold labour supply
Collective model
Chiappori (1992): equivalent to
maxCi,LiUi(Ci,Li)s.t.Ci+wiLi≤wiL0+Φi
where Φi describes how resources R1+R2 are shared in the household.
Intertemporal model
Intertemporal labour supply
Model
General utility function U(C0,…,CT;L0,…,LT) (intractable)
Separable utility function ∑Tt=0U(Ct,Lt,t)
Budget constraint At=(1+rt)At−1+Bt+wt(1−Lt)−Ct
- savings rate rt
- total time normalized to one: ht+Lt=1
- assets At
- non-labour income Bt
Intertemporal labour supply
Solution
L=∑tU(Ct,Lt,t)−∑tνt[At−(1+rt)At−1−Bt−wt(1−Lt)+Ct]
First-order conditions:
UL(Ct,Lt,t)UC(Ct,Lt,t)=wtνt=(1+rt+1)νt+1∀t∈[0,T]
Iterating over all periods: lnνt=−∑tτ=1ln(1+rτ)+lnν0
Intertemporal labour supply
Wage elasticities of labour supply
Frisch elasticity ψhw (holding νt constant)
Marshallian elasticity εhw (takes into account νt)
Hicksian elasticity ηhw (holding lifetime utility constant)
It is possible to show that ψhw≥ηhw≥εhw
Interpretation
Transitory changes in wages affect labour supply more than permanent changes.
Intertemporal labour supply
Example
Period utility U(Ct,Lt,t)=C1+ρt1+ρ−βtH1+γt1+γ
FOC: Hγt=1βtνtwt⇒lnHt=1γ(−lnβt+lnνt+lnwt)
- Evolutionary changes along anticipated wage profile ∂lnHt∂lnwt=1γ>0
- Transitory changes ∂lnHt∂lnwt=1γ(1+∂lnν0∂lnwt⏟<≈0)>0
- Permanent changes ∂lnHt∂lnwt=1γ(1+∂lnν0∂lnwt)≶0
- Lottery win ∂lnHt∂lnBt=1γ∂lnν0∂lnBt<0
Estimations
Empirical specifications
Basic regression equation
lnHit=αwlnwit+αRRit+θXit+vit
Interpretation of αw: Frisch, Marshallian or Hicksian? Depends on Rit!
Empirical specifications
Two-stage budgeting
Solution method of lifecycle labour supply models (Blundell and Macurdy 1999)
- Solve static labour supply model given Ct=Rt+wtHt
- Solve for series R1,…,RT to maximize lifetime utility
lnHit=αwlnwit+αR(Cit−witHit)+θXit+vit
Marshallian wage elasticity: αw
Income effect: αRwH
Hicksian wage elasticity: αw−αRwH
Empirical specifications
Frisch elasticity
Recall that lnνt=−∑tτ=1ln(1+rτ)+lnν0≡−ln(1+r)t+lnν0 (if rτ=r ∀τ)
Substitute αRRit=ρt+αRlnν0,i into basic equation:
lnHit=ρt+αwlnwit+αRlnν0,i+θXit+vitΔlnHit=ρ+αwΔlnwit+θΔXit+Δvit
Frisch wage elasticity: αw
Empirical specifications
Practical issues
Wages and hours worked are endogeneous
Hours (H|H>0) and participation (H>0)
Measurement errors
Measures of Cit
Individual vs aggregate labour supply
Estimates
Observational data
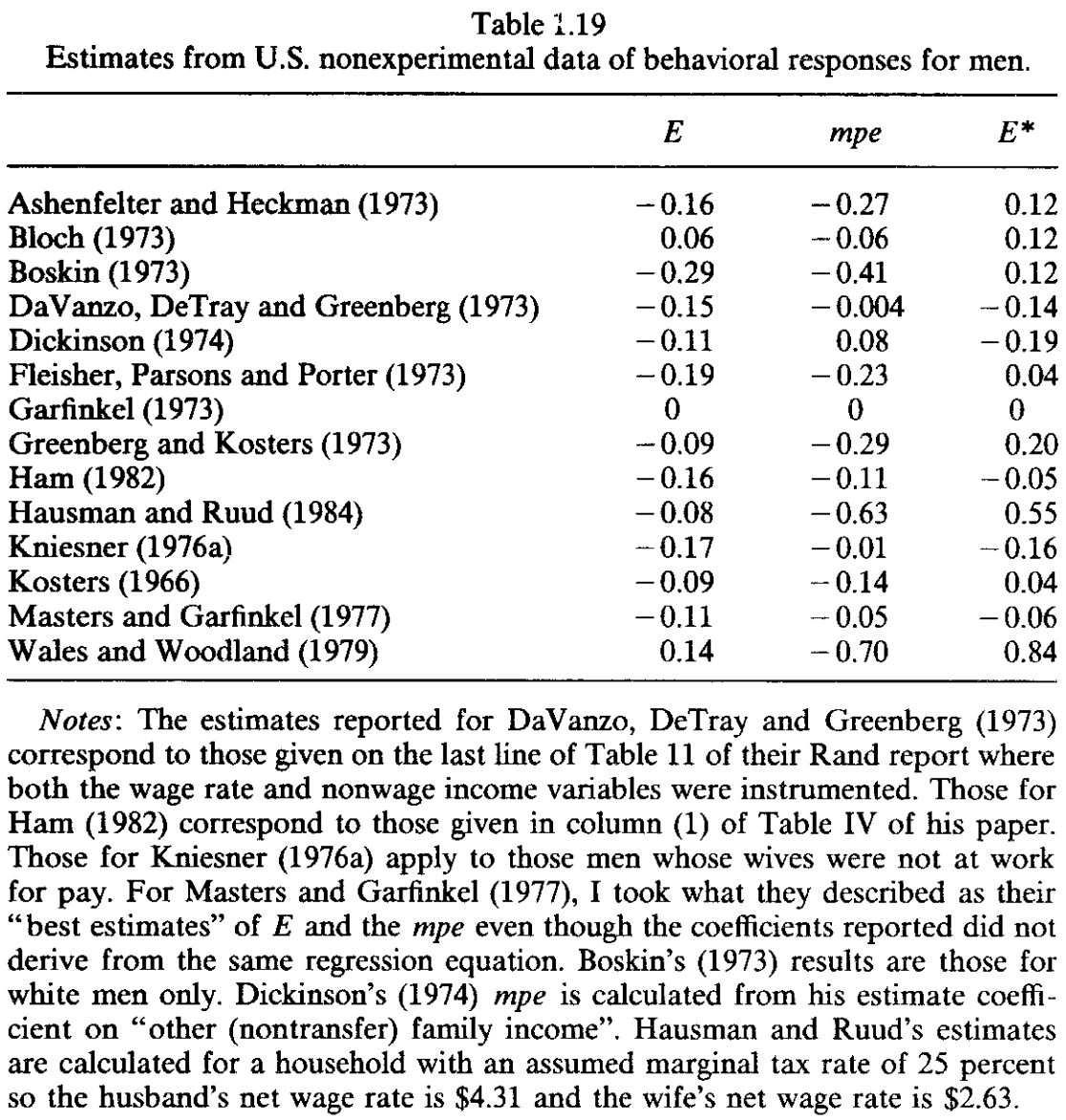
Source: Pencavel (1986)
Estimates
Experimental data: drop in tax rates in the UK 1978-92
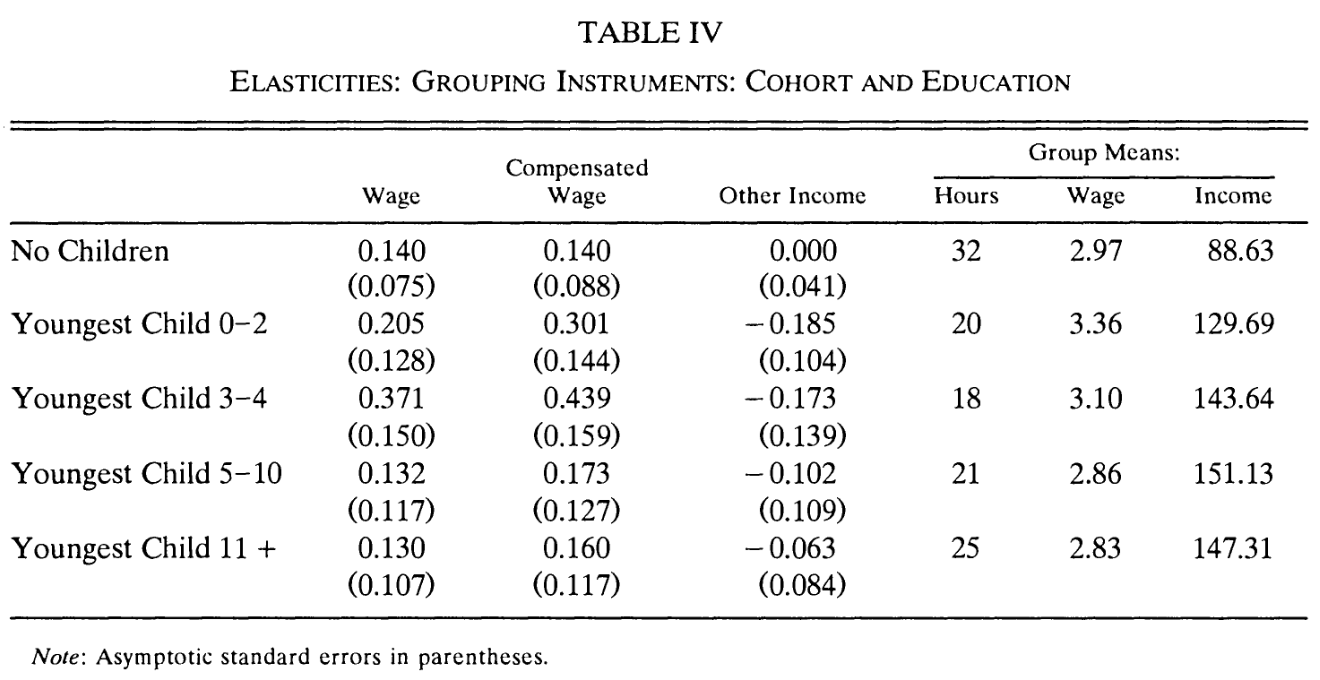
Source: Blundell, Duncan, and Meghir (1998)
Estimates
Intensive vs extensive margin

Source: Chetty et al. (2012)
Also some research on work effort for given hours of work (Dickinson 1999)
Estimates
Measurement errors
Classical measurement error in wit attenuates the estimate of αw
“Denominator bias” ↓αw if wages are computed as ratio of earning and hours with measurement errors. M. P. Keane (2011) computes average Hicksian elasticity
among all papers: 0.31
among papers with direct measure of wit: 0.43
Estimates
Measurement of consumption
PSID (US) dataset only includes food consumption data
| Consumption measure | Marshall | Hicks | Income | Frisch |
|---|---|---|---|---|
| PSID unadjusted | -0.442 | 0.094 | -0.536 | 0.148 |
| Food + imputed (food prices, demographics) | -0.468 | 0.328 | -0.796 | 0.535 |
| Food + imputed (house value, rent) | -0.313 | 0.220 | -0.533 | 0.246 |
Source: (M. P. Keane 2011, Table 5)
Estimates
Micro vs macro elasticities
Macro elasticities of labour supply typically higher than micro estimates
M. Keane and Rogerson (2012) highlight:
- extensive vs intensive margin
- model misspecification due to human capital accumulation
- aggregation is not straightforward
Estimates
Discrete choice dynamic programming
Incorporate discrete choices into model of labour supply
- labour force participation (Eckstein and Wolpin 1989)
- marriage (Van Der Klaauw 1996)
- fertility (Francesconi 2002)
M. P. Keane and Wolpin (2010) combine all + school and welfare participation choices
Summary
- Standard models of labour supply
- Static model
- Household model
- Intertemporal model
- Estimates of labour supply elasticities
- Typical issues encountered in data
- Variation in estimates and possible extensions
- Mostly covered seminal papers, but many ongoing works
- Tax and benefit policies
- Cross-wage elasticities
Next lecture: Labour Demand on 01 Sep